题目内容
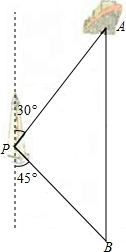 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为
如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为考点:解直角三角形的应用-方向角问题
专题:
分析:作PC⊥AB于C,由已知条件易求PC的长,在Rt△PBC中,PC=40,∠PBC=∠BPC=45°,则PB可求出.
解答:
解:作PC⊥AB于C,在Rt△PAC中,
∵PA=80,∠PAC=30°,
∴PC=40海里,
在Rt△PBC中,PC=40,∠PBC=∠BPC=45°,
∴PB=40
海里,
故答案为:40
.
∵PA=80,∠PAC=30°,

∴PC=40海里,
在Rt△PBC中,PC=40,∠PBC=∠BPC=45°,
∴PB=40
| 2 |
故答案为:40
| 2 |
点评:本题考查方位角、直角三角形、锐角三角函数的有关知识.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
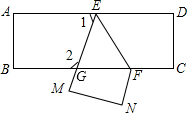 把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )
把一长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=50°,则∠1的度数是( )| A、90° | B、80° |
| C、70° | D、60° |
在(-1)3,(-1)2,-22,(-3)2这四个数中,最大的数与最小的数的积等于( )
| A、36 | B、9 | C、-9 | D、-36 |
 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,航向为北偏西n°,问:甲巡逻艇的航向?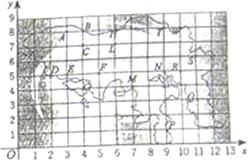 下图是画在方格纸上的某岛简图.
下图是画在方格纸上的某岛简图. 如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.
如图所示,△ABC中,三边分别是a,b,c,并且满足a2+b2-12a-16b+100=0,c=10.