题目内容
8.大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:| 销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
| 销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
分析 (1)待定系数法即可求得y与x的函数关系式;
(2)根据收支平衡关系列方程求得商品的成本a,根据毛利润=(售价-成本)×销售量-员工工资-应支付其它费用列函数关系式,配方后根据二次函数性质可得最值情况;
(3)由(2)中的最大毛利润,设需t天能还清借款,根据t天的总利润≥t天的本息和,列不等式求解即可.
解答 解:(1)由表可知,y是关于x的一次函数,设y=kx+b,
将x=110、y=50,x=115、y=45代入,
得:$\left\{\begin{array}{l}{110k+b=50}\\{115k+b=45}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=160}\end{array}\right.$,
∴y=-x+160;
(2)由已知可得:50×110=50a+3×100+200,
解得:a=100,
设每天的毛利润为W,
则W=(x-100)y-2×100-200
=(x-100)(-x+160)-2×100-200
=-x2+260x-16400
=-(x-130)2+500,
∴当x=130时,W取得最大值,最大值为500,
答:每件服装的销售价定为130元时,该服装店每天的毛利润最大,最大利润为500元;
(3)设需t天能还清借款,
则500t≥50000+0.0002×50000t
解得:t≥102$\frac{2}{49}$,
∵t为整数,
∴t的最小值为103,
答:该店最少需要103天才能还清集资款.
点评 本题考查了待定系数法求一次函数解析式、二次函数的应用及一元一次不等式的应用,理解题意依据相等关系或不等关系列出方程、函数关系式及不等式是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.超市招聘一名收银员,下面是三名应聘者各项测试成绩:
根据实际工作需要,该超市将计算机、商品知识和语言三项测试成绩按4:3:2的比例确定各人的素质测试成绩,三名应聘者中小赵将被录用.
| 素质测试 | 测试成绩/分 | ||
| 小李 | 小张 | 小赵 | |
| 计算机 | 80 | 70 | 85 |
| 商品知识 | 90 | 75 | 80 |
| 语言 | 85 | 80 | 95 |
17.在平面直角坐标系中,将点A(m-1,n+2)先向右平移3个单位,再向上平移2个单位,得到点A′,若点A′位于第二象限,则m、n的取值范围分别是( )
| A. | m<0,n>0 | B. | m<1,n>-2 | C. | m<0,n<-2 | D. | m<-2,m>-4 |
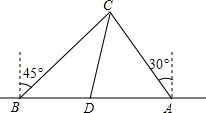 为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.
为了维护海洋权益,新组建的国家海洋局加大了在南海的巡逻力度,一天,我两艘海监船刚好在我某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍的船只停在C处海域.如图所示,AB=60($\sqrt{6}+\sqrt{2}$)海里,在B处测得C在北偏东45°的方向上,A处测得C在北偏西30°的方向上,在海岸线AB上有一灯塔D,测得AD=120($\sqrt{6}-\sqrt{2}$)海里.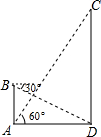 如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米.
如图,在数学活动课中,小敏为了测量校园内旗杆CD的高度,先在教学楼的底端A点处,观测到旗杆顶端C的仰角∠CAD=60°,然后爬到教学楼上的B处,观测到旗杆底端D的俯角是30°,已知教学楼AB高4米. 如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.
如图,在⊙O的内接五边形ABCDE中,∠CAD=40°,则∠B+∠E=220°.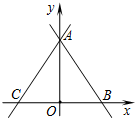 如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3.
如图,直线AB的函数关系式为y=-$\frac{3}{2}$x+3,直线AC与直线AB关于y轴成轴对称,则直线AC的函数关系式为y=$\frac{3}{2}$x+3. 如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)
如图所示,某数学活动小组要测量山坡上的电线杆PQ的高度,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为31°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是68°,求信号塔PQ的高度.(结果精确到0.1米,参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.48,tan31°≈0.60,sin31°≈0.52,cos31°≈0.86)