题目内容
1.点A为直线l外一点,点B和点C在直线l上,A,B,C三点所围成的三角形的面积是10,BC=5,则点A到直线l的距离为4.分析 根据三角形的面积是10,BC=5,求出BC边上的高,即为点A到直线l的距离.
解答 解:BC边上的高为:10×2÷5=4,
则点A到直线l的距离为4,
故答案为:4.
点评 本题考查了点到直线的距离,解决本题的关键是熟记点到直线的距离的定义.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.已知x>y,m≠0,则下列说法中,正确的是( )
| A. | m+x>m+y | B. | m-x>m-y | C. | mx>my | D. | m2x≥m2y |
6.-3的相反数的倒数是( )
| A. | 3 | B. | -|-3| | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
11.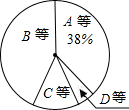 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
(1)在被调查的男生中,成绩为B等级的有23人,占被调查男生人数的46%,m=0.38;
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
 某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).
某校为了解七年级男生体操测试情况,随机抽取了50名男生的测试成绩进行统计,根据评分标准,将他们的成绩分为A,B,C,D四个等级,并绘制成频数分布表和扇形统计图(如图).| 等级 | 成绩x/分 | 频数/(人数) | 频率 |
| A | 9.0≤x≤10.0 | a | m |
| B | 7.0≤x<9.0 | 23 | 0.46 |
| C | 6.0≤x<7.0 | b | n |
| D | 0.0≤x<6.0 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(2)求a,b,n的值;
(3)如果该校七年级共有200名男生,试估计这200名男生中成绩达到A等级和B等级的共有多少人.
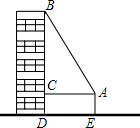 如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?
如图,一高层住宅发生火灾,消防车立即赶到距大厦5米处(车尾AE到大厦墙面CD的距离为5米),升起云梯到火灾窗口B,已知云梯AB长13米,云梯底部距地面的高AE为3米,求发生火灾的住户窗口距地面的高BD是多少米?


