题目内容
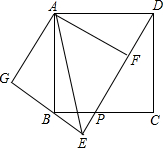 如图,四边形ABCD是正方形,点P在BC上,点F在DP上,将△ADF绕点A顺时针针旋转到△ABG,GB与DP的延长线交于点E.
如图,四边形ABCD是正方形,点P在BC上,点F在DP上,将△ADF绕点A顺时针针旋转到△ABG,GB与DP的延长线交于点E.(1)求证:GE⊥DE;
(2)若AE=mEG,探究EG与EF的数量关系,并证明你的结论.
考点:正方形的性质,勾股定理
专题:
分析:(1)根据旋转的性质得出∠GAB=∠FAD,∠G=∠AFD,进而求得∠GAF=90°∠G+∠AFE=180°,根据四边形的内角和360°,即可求得∠GEF=90°,进而求得GE⊥DE.
(2)作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,从而证得△AMG≌△ANF和四边形AMEN是正方形,进一步证得MG=NF,AM=AN,证得EF=EG+2MG,ME=MG+EG=
AE,根据已知得出MG=(
m-1)EG,即可证得EF=(
m-)EG.
(2)作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,从而证得△AMG≌△ANF和四边形AMEN是正方形,进一步证得MG=NF,AM=AN,证得EF=EG+2MG,ME=MG+EG=
| ||
| 2 |
| ||
| 2 |
| 2 |
解答:(1)证明:∵△AGB≌△AFD,
∴∠GAB=∠FAD,∠G=∠AFD,
∵∠BAD=∠FAD+∠BAF=90°,∠AFD+∠AFE=90°,
∴∠GAB+∠BAF=90°,
∴∠GAF=90°∠G+∠AFE=180°,
∴∠GEF=90°,
∴GE⊥DE;
(2)如图,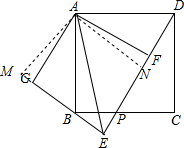 作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,
作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,
∴∠AGM=∠AEN,
在△AMG与△ANF中,
,
∴△AMG≌△ANF(AAS),
∴MG=NF,AM=AN,
∵∠AME=∠ANE=∠GEF=90°,
∴四边形AMEN是正方形,
∴AM=AN=ME=EN,
∴EF=EG+2MG,ME=MG+EG=
AE,
∵AE=mEG,
∴MG+EG=
•mEG,
∴MG=(
m-1)EG,
∴EF=EG+2MG=EG+2(
m-1)EG=(
m-1)EG,
即EF=(
m-)EG.
∴∠GAB=∠FAD,∠G=∠AFD,
∵∠BAD=∠FAD+∠BAF=90°,∠AFD+∠AFE=90°,
∴∠GAB+∠BAF=90°,
∴∠GAF=90°∠G+∠AFE=180°,
∴∠GEF=90°,
∴GE⊥DE;
(2)如图,
 作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,
作AM⊥GE,交EG的延长线于M,作AN⊥ED于N,∴∠AGM=∠AEN,
在△AMG与△ANF中,
|
∴△AMG≌△ANF(AAS),
∴MG=NF,AM=AN,
∵∠AME=∠ANE=∠GEF=90°,
∴四边形AMEN是正方形,
∴AM=AN=ME=EN,
∴EF=EG+2MG,ME=MG+EG=
| ||
| 2 |
∵AE=mEG,
∴MG+EG=
| ||
| 2 |
∴MG=(
| ||
| 2 |
∴EF=EG+2MG=EG+2(
| ||
| 2 |
| 2 |
即EF=(
| 2 |
点评:本题考查了正方形的判定和性质,全等三角形的判定和性质,旋转的性质,勾股定理的应用等,作出辅助线构建正方形是本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
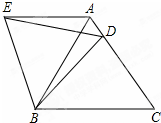 如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=5,BD=4,则△AED的周长是
如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=5,BD=4,则△AED的周长是 如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=BD=4,∠A=30°,
如图,点B在⊙O的直径AC的延长线上,点D在⊙O上,AD=BD=4,∠A=30°,