题目内容

已知在Rt△ABC中，CD⊥AB于D，DE⊥AC于E，求证：
AC•AC
BC•BC
=
AE
CE
．
考点：相似三角形的判定与性质
专题：证明题
分析：首先利用相似三角形的性质求出所证明的等式左边与线段AD、CD之间的关系，然后借助射影定理即可解决问题．
解答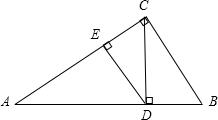：证明：如图，∵△ABC是直角三角形，且CD⊥AB，
∴∠A+∠B=∠DCB+∠B，
故∠A=∠DCB；
又∵∠ADC=∠CDB=90°，
∴△ADC∽△CDB，
AC
BC
=
AD
CD
，
∴
AC2
BC2
=
AD2
CD2
；
又∵DE⊥AC，
∴AD2=AE•AC，CD2=CE•AC（射影定理），
∴
AD2
CD2
=
AE•AC
CE•AC
=
AE
CE
，
故
AC2
BC2
=
AE
CE
；
 即
AC•AC
BC•BC
=
AE
CE
．
点评：考查了相似三角形的判定及其性质的应用问题；同时还渗透了对射影定理的考查，对综合变形能力提出了较高的要求．
练习册系列答案
相关题目
某书城开展学生优惠售书活动，凡一次性购书不超过200元的一律九折优惠；超过200元的，其中200元按九折算，超过200元的按八折算．李明购书后付了212元，若没有任何优惠，则李明应该付多少元？
把（a+b）和（x+y）各看成一个整体，对下列各式进行化简：
（1）4（a+b）+2（a+b）-（a+b）；
（2）3（x+y）2-7（x+y）+8（x+y）2+6（x+y）
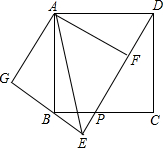如图，四边形ABCD是正方形，点P在BC上，点F在DP上，将△ADF绕点A顺时针针旋转到△ABG，GB与DP的延长线交于点E．
（1）求证：GE⊥DE；
（2）若AE=mEG，探究EG与EF的数量关系，并证明你的结论．
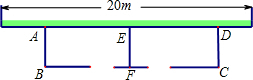如图，利用一面墙（墙的长度为20m），用34m长的篱笆围成两个鸡场，中间用一道篱笆隔开，每个鸡场均留一道1m宽的门，设AB的长为x米．
（1）若两个鸡场总面积为96m2，求x；
（2）若两个鸡场的面积和为S，求S关于x的关系式；
（3）两个鸡场面积和S有最大值吗？若有，最大值是多少？
探究与发现：
探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？

已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．
探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．
探究三：若将△ADC改为任意四边形ABCD呢？
已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．
阅读下面的材料：
∵ax2+bx+c=0（a≠0）的根为：x1=
-b+
b2-4ac
2a
，x2=
-b-
b2-4ac
2a
，
∴x1+x2=
-2b
2a
=-
b
a
，x1•x2=
b2-(b2-4ac)
4a2
=
c
a
，
综上得，设ax2+bx+c=0（a≠0）的两根为x1、x2，则有：x1+x2=-
b
a
，x1x2=
c
a
，请利用这一结论解决问题：
（1）若x2+bx+c=0的两根为1和3，求b和c的值．
（2）设方程2x2+3x+1=0的根为x1、x2，求x12+x22的值．
一元二次方程x2+kx-3=0的一个根是x1=1，则另一个根是（　　）
A、2B、-2C、3D、-3
若（mx+8）（2-3x）展开后不含x的一次项，则m=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网