题目内容
在等边△ABC中,D为BC上一点,BD=2CD,DE⊥AB于点E,CE交AD于点P,求∠APE的度数.
考点:全等三角形的判定与性质,等边三角形的性质,含30度角的直角三角形
专题:
分析:如图,根据等边三角形的性质就可以得出∠B=∠ACB=60°,BC=AC,再由直角三角形BED中,30度所对的直角边等于斜边的一半得到BD=2BE,由BD=2CD,等量代换得到BE=CD,利用SAS得到三角形BEC与三角形ADC全等,利用全等三角形对应角相等得到∠BCE=∠DAC,利用内角和定理及外角性质即可确定出所求角的度数.
解答: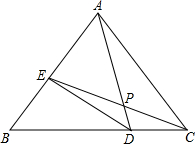 解:如图所示,
解:如图所示,
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC=BC,
∵DE⊥AB,
∴∠DEB=90°,
在Rt△BDE中,∠BDE=30°,
∴BD=2BE,
∵BD=2DC,
∴BE=DC,
在△BEC和△CDA中,
,
∴△BEC≌△CDA(SAS),
∴∠BCE=∠CAD,
∴∠ADC+∠BCE=∠ADC+∠CAD=180°-∠ACB=120°,
∵∠APC为△PDC的外角,
∴∠APC=∠ADC+∠BCE=120°,
则∠APE=60°.
 解:如图所示,
解:如图所示,∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°,AB=AC=BC,
∵DE⊥AB,
∴∠DEB=90°,
在Rt△BDE中,∠BDE=30°,
∴BD=2BE,
∵BD=2DC,
∴BE=DC,
在△BEC和△CDA中,
|
∴△BEC≌△CDA(SAS),
∴∠BCE=∠CAD,
∴∠ADC+∠BCE=∠ADC+∠CAD=180°-∠ACB=120°,
∵∠APC为△PDC的外角,
∴∠APC=∠ADC+∠BCE=120°,
则∠APE=60°.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
烟花厂为雁荡山旅游节特别设计制作一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=-
t2+20t+1,若这种礼炮在点火升空到最高点处引爆,则从点火升空到引爆需要的时间为( )
| 5 |
| 2 |
| A、3s | B、4s | C、5s | D、6s |
如果
是二次根式,那么a应满足( )
| a-3 |
| A、a≥0 | B、a≠3 |
| C、a=3 | D、a≥3 |
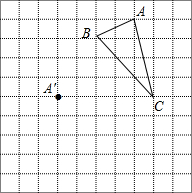 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.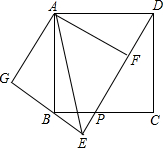 如图,四边形ABCD是正方形,点P在BC上,点F在DP上,将△ADF绕点A顺时针针旋转到△ABG,GB与DP的延长线交于点E.
如图,四边形ABCD是正方形,点P在BC上,点F在DP上,将△ADF绕点A顺时针针旋转到△ABG,GB与DP的延长线交于点E.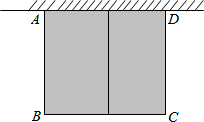 如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,
如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米).如果AB的长为x,面积为y,