题目内容
13.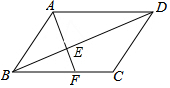 在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( )
在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( )| A. | 12 | B. | 24 | C. | 13 | D. | 26 |
分析 由相似三角形△AED∽△FEB的性质可以求得△AED的面积,然后由△ABE与△AED是同高的两个三角形,易得△ABE的面积,所以S?ABCD=2(S△ABE+S△AED).
解答  解:如图,∵BD=4BE,
解:如图,∵BD=4BE,
∴$\frac{DE}{BE}$=3,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴△AED∽△FEB,
∴$\frac{{S}_{△AED}}{{S}_{△FEB}}$=($\frac{DE}{BE}$)2=9.
∵△BEF的面积为1,
∴S△AED=9.
又∵S△ABE=$\frac{1}{3}$S△AED=3.
∴S?ABCD=2(S△ABE+S△AED)=2×(3+9)=24.
故选:B.
点评 本题考查平行四边形的性质,相似三角形的判定和性质,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,掌握同高异底的两个三角形的面积比等于底的比,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如图反映2001至2005年间某市居民人均收入的年增长率.下列说法正确的是( )


| A. | 2003年农村居民人均收入低于2002年 | |
| B. | 农村居民人均收入年增长率低于9%的有2年 | |
| C. | 农村居民人均收入最多的是2004年 | |
| D. | 农村居民人均收入在逐年增加 |

 如图,点E是?ABCD的边AD的中点,BE与AC相交于点P,则S△APE:S△BCP=1:4.
如图,点E是?ABCD的边AD的中点,BE与AC相交于点P,则S△APE:S△BCP=1:4.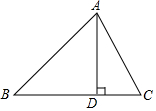 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.