题目内容
18.阅读下面材料:在数学课上,老师给同学们布置了一道尺规作图题:尺规作图:作Rt△ABC,使其斜边AB=c,一条直角边BC=a.已知:如图1,正比例函数和反比例函数的
图象分别交于M、N两点.
要求:在y轴上求作点P,使得∠MPN为直角.
小丽的作法如下:如图2,以点O为圆心,以OM长为半径作⊙O,
⊙O与y轴交于P1、P2两点,则点P1、P2即为所求.
老师说:“小丽的作法正确.”
请回答:小丽这样作图的依据是半圆(或直径)所对的圆周角是直角.

分析 根据半圆(或直径)所对的圆周角是直角可知,以MN为直径作圆即可.
解答 解:因为反比例函数与正比例函数都是中心对称图形,对称中心是原点O,
所以OM=ON,以点O为圆心,以OM长为半径作⊙O,
⊙O与y轴交于P1、P2两点,则点P1、P2即为所求,
理由:半圆(或直径)所对的圆周角是直角.
故答案为半圆(或直径)所对的圆周角是直角.
点评 本题考查考查反比例函数与一次函数的交点,圆的有关性质等知识,解题的关键是熟练应用所学知识解决问题,属于基础题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
9.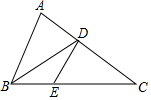 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )| A. | 4 | B. | 6 | C. | $\frac{5}{3}$ | D. | $\frac{10}{3}$ |
3. 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
 小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )
小聪用直尺和圆规作角平分线,方法如下:①利用三角板上的刻度,在OA和OB上分别截取OM、ON,使OM=ON;②分别过M、N作OM、ON的垂线,交于点P;③作射线OP,则OP为∠AOB的平分线,小聪用尺规作角平分线时,用到的三角形全等的判定方法是( )| A. | SSS | B. | SAS | C. | ASA | D. | HL |
10.根据等式的性质,下列各式的变形中,一定正确的是( )
| A. | 若a=b,则a+c=b-c | B. | 若a=b+2,则3a=3b+6 | ||
| C. | 若6a=2b,则a=3b | D. | 若ac=bc,则a=b |
7.点(-1,-$\sqrt{2}$)所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.分解因式a2b-b3结果正确的是( )
| A. | b(a+b)(a-b) | B. | b(a-b)2 | C. | b(a2-b2) | D. | b(a2+b2) |
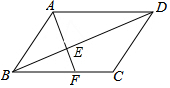 在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( )
在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( )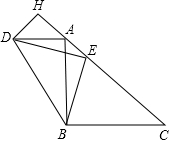 如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.
如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H. 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.
如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画出了一个与书上完全一样的三角形,那么亮亮画图的依据是两角和它们的夹边分别相等的两个三角形全等.