题目内容
2.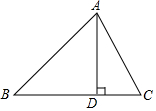 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
分析 设BD=x,由CD=BC-BD表示出CD,分别在直角三角形ABD与直角三角形ACD中,利用勾股定理表示出AD2,列出关于x的方程,求出方程的解得到AD的长,即可求出三角形ABC面积.
解答 解:如图,在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14-x,
由勾股定理得:AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
∴152-x2=132-(14-x)2,
解之得:x=9,
∴AD=12,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×14×12=84.
点评 此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
相关题目
12. 如图,在研究用火柴摆正方形的问题时,
如图,在研究用火柴摆正方形的问题时,
小明认为摆n个正方形需(3n+1)根火柴棒;
小凡认为摆n个正方形需[n+n+(n+1)]根火柴棒;
小亮认为摆n个正方形需(4n-n)根火柴棒;
小刚认为摆n个正方形需(n+n+n)根火柴棒.
你认为他们谁说的对( )
 如图,在研究用火柴摆正方形的问题时,
如图,在研究用火柴摆正方形的问题时,小明认为摆n个正方形需(3n+1)根火柴棒;
小凡认为摆n个正方形需[n+n+(n+1)]根火柴棒;
小亮认为摆n个正方形需(4n-n)根火柴棒;
小刚认为摆n个正方形需(n+n+n)根火柴棒.
你认为他们谁说的对( )
| A. | 小明说的对 | B. | 四位同学说的都对 | ||
| C. | 小明、小凡说得对 | D. | 小亮、小刚说的对 |
9.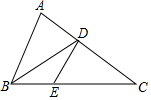 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
 如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )
如图,△ABC中,BD是∠ABC的平分线,DE∥AB交BC于E,EC=3,BE=2,则AB=( )| A. | 4 | B. | 6 | C. | $\frac{5}{3}$ | D. | $\frac{10}{3}$ |
7.点(-1,-$\sqrt{2}$)所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
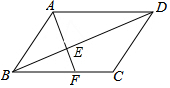 在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( )
在?ABCD中,E为BD上一点,在连结AE并延长交BC于F点,且BD=4BE,△BEF的面积为1,则?ABCD的面积为( ) 如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°.
如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=140°,则∠AOC=55°;∠BOC=35°.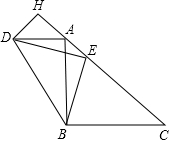 如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.
如图,在△ABC中,BA=BC,∠ABC=90°,AD∥BC,点E在边AC上,且∠DEB=90°,DH⊥AC于H.