从多边形一条边上的一点出发.连接各个顶点得到2013个三角形.则这个多边形的边数为( )A．2 011B．2 015C．2 014D．2 016 题目和参考答案——青夏教育精英家教网—

题目内容

17．从多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2013个三角形，则这个多边形的边数为（　　）

A．

2 011

B．

2 015

C．

2 014

D．

2 016

分析可根据多边形的一点（不是顶点）出发，连接各个顶点得到的三角形个数与多边形的边数的关系求解．

解答解：多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2013个三角形，
则这个多边形的边数为2013+1=2014．
故选：C．

点评此题考查了规律型：图形的变化，多边形一条边上的一点（不是顶点）出发，连接各个顶点得到的三角形个数=多边形的边数-1．

练习册系列答案

活页英语时文阅读理解系列答案

火辣英语初中阅读理解与完形填空系列答案

交大之星现代文经典阅读300题系列答案

开卷8分钟英语阅读理解与完形填空系列答案

开路先锋系列答案

课内外文言文阅读系列答案

相关题目

7．

如图，在△ABC中，∠ACB=70°，∠1=∠2，则∠BPC的度数为（　　）

8．已知|x|=4，|y|=$\frac{1}{4}$，xy＜0，则x+y=±$\frac{15}{4}$．

5．

如图，AD∥BC，AB∥DC，则全等三角形共有4对．

12．计算：
①-17-（-23）-53+36
②-81÷2$\frac{1}{4}$-（-$\frac{8}{3}$）÷（-16）
③（$\frac{2}{3}$-$\frac{1}{4}$-$\frac{3}{8}$+$\frac{5}{24}$）×（-48）
④-2²×（-$\frac{1}{2}$）+8÷（-2）²
⑤（-1）²⁰⁰⁸+（-5）×[（-2）³+2]-（-4）²÷（-$\frac{1}{2}$）

2．已知a＞0，b＜0，且|b|＞|a|，则a，-a，b，-b按从小到大的顺序排列（　　）

	A．	数轴上任何一个点都表示唯一的有理数
	B．	两个无理数的乘积一定是无理数
	C．	两个无理数之和一定是无理数
	D．	数轴上的点和实数是一一对应的

6．下列说法中，正确的是（　　）

	A．	两边及其中一边的对角分别相等的两个三角形全等
	B．	两边及其中一边上的高分别相等的两个三角形全等
	C．	斜边和一锐角分别相等的两个直角三角形全等
	D．	面积相等的两个三角形全等

7．

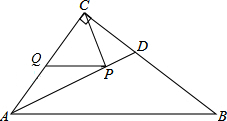如图，在Rt△ABC中，∠ACB=90°，∠B=30°，BC=8，AD是∠BAC的平分线，若点P，Q分别是AD和AC上的动点，则PC+PQ的最小值是4．

试题分类