题目内容
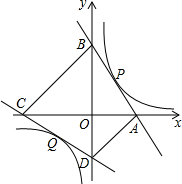 如图,一次函数y=-
如图,一次函数y=-| 3 |
| 2 |
| k |
| x |
(1)求k的值;
(2)若一次函数y=mx+n的图象与y=
| k |
| x |
(3)求四边形ABCD的最小面积.
考点:反比例函数综合题,根的判别式,平行线的判定,相似三角形的判定与性质
专题:综合题,配方法
分析:(1)可先求出点A、B的坐标,再求出线段AB的中点P的坐标,然后把点P的坐标代入y=
就可求出k;
(2)可先求出点C、D的坐标(用m、n的代数式表示),然后根据两个函数图象在第三象限只有一个公共点,运用根的判别式可得到n2=-24m,从而可得到OC•OD=24=OA•OB,从而可证到△AOD∽△COB,则有∠ADO=∠CBO,从而可得AD∥BC;
(2)易得S四边形ABCD=
AC•BD=
(4+
)(6-n),然后把m=-
代入,就可得到S四边形ABCD与n的关系,然后只需运用配方法即可解决问题.
| k |
| x |
(2)可先求出点C、D的坐标(用m、n的代数式表示),然后根据两个函数图象在第三象限只有一个公共点,运用根的判别式可得到n2=-24m,从而可得到OC•OD=24=OA•OB,从而可证到△AOD∽△COB,则有∠ADO=∠CBO,从而可得AD∥BC;
(2)易得S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| m |
| n2 |
| 24 |
解答:解:(1)对于一次函数y=-
x+6,
当x=0时,y=-
×0+6=6,则有B(0,6),OB=6;
当y=0时,-
x+6=0,解得x=4,则有A(4,0),OA=4.
∴线段AB的中点P坐标为(
,
)即(2,3).
∵P在反比例函数y=
的图象上,
∴k=xy=2×3=6,
∴k的值为6;
(2)对于一次函数y=mx+n,
当x=0时,y=m×0+n=n,则有D(0,n),OD=-n;
当y=0时,mx+n=0,解得x=-
,则有C(-
,0),OC=
.
∵一次函数y=mx+n的图象与y=
的图象有且只有一个第三象限的公共点Q,
∴方程mx+n=
即mx2+nx-6=0有两个相等的实数根,
∴n2-4×m×(-6)=n2+24m=0,
∴n2=-24m,
∴OC•OD=
×(-n)=-
=24.
∵OA•OB=4×6=24,
∴OA•OB=OC•OD,
∴
=
.
∵∠AOD=∠COB=90°,
∴△AOD∽△COB,
∴∠ADO=∠CBO,
∴AD∥BC,
∴AD与BC的位置关系是AD∥BC;
(3)S四边形ABCD=S△ABC+S△ADC=
AC•OB+
AC•OD=
AC•BD
=
×[4-(-
)]×[6-n]=
(4+
)(6-n)
=
(24-4n+
-
)=
(24-4n+
-
)
=
(24-4n-
+24)
=24-2n-
=24+2[(
)2+(
)2]
=24+2[(
-
)2+12]
=24+2(
-
)2+24
=48+2(
-
)2,
∴当
=
即n=-6时,S四边形ABCD取到最小值48.
∴四边形ABCD的最小面积为48.
| 3 |
| 2 |
当x=0时,y=-
| 3 |
| 2 |
当y=0时,-
| 3 |
| 2 |
∴线段AB的中点P坐标为(
| 4+0 |
| 2 |
| 0+6 |
| 2 |
∵P在反比例函数y=
| k |
| x |
∴k=xy=2×3=6,
∴k的值为6;
(2)对于一次函数y=mx+n,
当x=0时,y=m×0+n=n,则有D(0,n),OD=-n;
当y=0时,mx+n=0,解得x=-
| n |
| m |
| n |
| m |
| n |
| m |
∵一次函数y=mx+n的图象与y=
| 6 |
| x |
∴方程mx+n=
| 6 |
| x |
∴n2-4×m×(-6)=n2+24m=0,

∴n2=-24m,
∴OC•OD=
| n |
| m |
| n2 |
| m |
∵OA•OB=4×6=24,
∴OA•OB=OC•OD,
∴
| OA |
| OC |
| OD |
| OB |
∵∠AOD=∠COB=90°,
∴△AOD∽△COB,
∴∠ADO=∠CBO,
∴AD∥BC,
∴AD与BC的位置关系是AD∥BC;
(3)S四边形ABCD=S△ABC+S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| n |
| m |
| 1 |
| 2 |
| n |
| m |
=
| 1 |
| 2 |
| 6n |
| m |
| n2 |
| m |
| 1 |
| 2 |
| 6n | ||
-
|
| -24m |
| m |
=
| 1 |
| 2 |
| 144 |
| n |
=24-2n-
| 72 |
| n |
=24+2[(
| -n |
| 6 | ||
|
=24+2[(
| -n |
| 6 | ||
|
=24+2(
| -n |
| 6 | ||
|
=48+2(
| -n |
| 6 | ||
|
∴当
| -n |
| 6 | ||
|
∴四边形ABCD的最小面积为48.
点评:本题主要考查了直线与反比例函数图象上点的坐标特征、用待定系数法求k的值、根的判别式、相似三角形的判定与性质、平行线的判定、中点坐标公式等知识,运用根的判别式得到n2=-24m,从而得到OC•OD=OA•OB是解决第(2)小题的关键,运用割补法及配方法是解决第(3)小题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.
如图,AC平分∠DAB,∠1=∠2,试说明AB与CD的位置关系,并予以证明.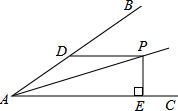 若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE=
若∠BAC=30°,AP平分∠BAC,PD∥AC且PD=5,PE⊥AC于E,则PE= 如图,将直角三角形ABC沿射线BC的方向平移得到△DEF,求图中阴影部分的面积.
如图,将直角三角形ABC沿射线BC的方向平移得到△DEF,求图中阴影部分的面积.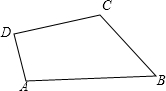 如图,四边形ABCD中,∠D=90°,AB=3,BC=CD=2,AD=1.求四边形ABCD的面积.
如图,四边形ABCD中,∠D=90°,AB=3,BC=CD=2,AD=1.求四边形ABCD的面积.