题目内容
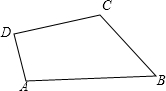 如图,四边形ABCD中,∠D=90°,AB=3,BC=CD=2,AD=1.求四边形ABCD的面积.
如图,四边形ABCD中,∠D=90°,AB=3,BC=CD=2,AD=1.求四边形ABCD的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:先根据勾股定理求出AC的长,再由勾股定理的逆定理判断出△ABC的形状,根据三角形的面积公式即可得出结论.
解答: 解:∵连接AC,
解:∵连接AC,
∵∠D=90°,AD=1,CD=2,
∴AC=
=
=
.
∵AB=3,BC=2,AC=
,22+(
)2=32,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC=
×1×2+
×2×
=1+
.
 解:∵连接AC,
解:∵连接AC,∵∠D=90°,AD=1,CD=2,
∴AC=
| AD2+CD2 |
| 12+22 |
| 5 |
∵AB=3,BC=2,AC=
| 5 |
| 5 |
∴△ABC是直角三角形,
∴S四边形ABCD=S△ACD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
下列4个数-5,3,0,-2中,最大的数是( )
| A、-5 | B、3 | C、0 | D、-2 |
函数y=
中自变量x的取值范围是( )
| 2x-1 |
A、x≥-
| ||
B、x≥
| ||
| C、x≤-2 | ||
| D、x≤2 |
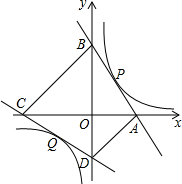 如图,一次函数y=-
如图,一次函数y=- 如图,直线l与x轴、y轴交于A、B两点,且A(4,0),B(0,3),则这条直线关于y轴对称的直线l1的解析式为
如图,直线l与x轴、y轴交于A、B两点,且A(4,0),B(0,3),则这条直线关于y轴对称的直线l1的解析式为