题目内容
已知下列命题:①对角线垂直且相等的四边形是正方形,②平分弦的直径垂直于弦,③对角互补的四边形内接与圆,④无理数是无限小数,其中原命题和逆命题均为真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题与定理
专题:
分析:先分别根据正方形的判定、垂径定理和无理数的定义判定①②④为假命题;根据四点共圆的条件和圆内接四边形的性质对③和它的逆命题进行判断.
解答:解:对角线互相垂直平分且相等的四边形是正方形,所以①为假命题;
平分弦(非直径)的直径垂直于弦,所以②为假命题;
对角互补的四边形内接与圆,所以③为真命题,其逆命题为圆的内接四边形的对角互补,这个逆命题为真命题;
无理数是无限不循环小数,所以④为假命题.
故选A.
平分弦(非直径)的直径垂直于弦,所以②为假命题;
对角互补的四边形内接与圆,所以③为真命题,其逆命题为圆的内接四边形的对角互补,这个逆命题为真命题;
无理数是无限不循环小数,所以④为假命题.
故选A.
点评:本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了逆定理.

练习册系列答案
相关题目
下列4个数-5,3,0,-2中,最大的数是( )
| A、-5 | B、3 | C、0 | D、-2 |
函数y=
中自变量x的取值范围是( )
| 2x-1 |
A、x≥-
| ||
B、x≥
| ||
| C、x≤-2 | ||
| D、x≤2 |
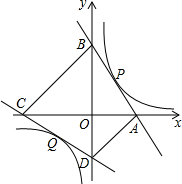 如图,一次函数y=-
如图,一次函数y=-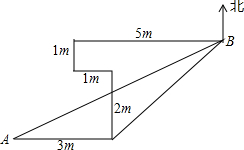 如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.
如图,小林在平坦的场地上从A点向东走了3m,再向北走了2m,再向西走了1m,又向北走了1m,最后向东走了5m,到达B点,求A、B之间的距离.