题目内容
20.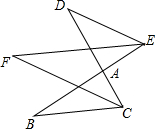 如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F
如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F(1)如果∠B=32°,∠D=38°,求∠F的度数;
(2)求证:∠F=$\frac{1}{2}$(∠B+∠D).
分析 (1)在△ABC和△ADE中,根据三角形的内角和定理表示出∠ACB和∠AED的关系,然后根据角平分线的定义表示出∠BCF和∠BEF,然后再次利用三角形的内角和定理列式整理即可得解;
(2)在△ABC和△ADE中,根据三角形的内角和定理表示出∠ACB和∠AED的关系,然后根据角平分线的定义表示出∠BCF和∠BEF,然后再次利用三角形的内角和定理列式整理即可得证.
解答 (1)解:在△ABC和△ADE中,∠B+∠ACB=∠D+∠AED,
∵∠B=32°,∠D=38°,
∴32°+∠ACB=38°+∠AED,
∴∠ACB=6°+∠AED,
∵∠DEA、∠BCA的平分线相交于F,
∴∠BCF=$\frac{1}{2}$∠ABC,∠BEF=$\frac{1}{2}$∠AED,
∵∠F+∠BEF=∠B+∠BCF,
∴∠F+$\frac{1}{2}$∠AED=32°+$\frac{1}{2}$∠ABC,
∴∠F+$\frac{1}{2}$∠AED=32°+$\frac{1}{2}$(∠AED+6°),
解得∠F=35°;
(2)证明:在△ABC和△ADE中,∠B+∠ACB=∠D+∠AED,
∵∠DEA、∠BCA的平分线相交于F,
∴∠BCF=$\frac{1}{2}$∠ABC,∠BEF=$\frac{1}{2}$∠AED,
∵∠F+∠BEF=∠B+∠BCF,
∴∠F+$\frac{1}{2}$∠AED=∠B+$\frac{1}{2}$∠ABC,
∴∠F+$\frac{1}{2}$∠AED=∠B+$\frac{1}{2}$(∠AED+∠D-∠B),
∴∠F=$\frac{1}{2}$(∠B+∠D).
点评 本题考查了三角形的内角和定理,角平分线的定义,根据“八字形”图形的对顶角相等利用三角形的内角和定理列出等式是解题的关键,要注意整体思想的利用.

 甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.
甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.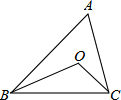 已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.
已知:如图:△ABC中,∠B、∠C的角平分线交于点O,若∠A=60°,则∠BOC=120°.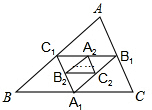 如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的面积是32,△A1B1C1的面积是S1,△A2B2C2的面积是S2,…,则△A4B4C4的面积S4=$\frac{1}{8}$.
如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的面积是32,△A1B1C1的面积是S1,△A2B2C2的面积是S2,…,则△A4B4C4的面积S4=$\frac{1}{8}$.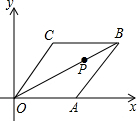 如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,菱形OABC的顶点A在x轴上,顶点B的坐标为(8,4)点P的对角线OB上一个动点,点D的坐标为(0,-2),当DP与AP之和最小时,点P的坐标为($\frac{4}{3}$,$\frac{2}{3}$).