题目内容
10. 甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.
甲骑摩托车从A地去B地,乙开汽车从B地丢A地,同时出发.匀速行驶.各自列达终点后停止.设甲、乙两人间距离为S(单位:千米),甲行驶的时间为t(单位:小时).变量s与t之间的关系如图所示.(1)求甲、乙各自的速度;
(2)求甲出发后在什么时间甲、乙两人相距100千米.
分析 (1)根据图象知,甲行驶全程120千米时间为1.5小时可得甲的速度,根据t=1时甲、乙两人相遇列方程可得乙的速度;
(2)分别求出0≤t≤1、1.5≤t≤3时s与t的函数关系式,令s=100可得t的值.
解答 解:(1)甲骑摩托车的速度为:120÷3=40(千米/小时),设乙开汽车的速度为a千米/小时,则:40+a=120,
解得:a=80,
∴乙开汽车的速度为80千米/小时,
答:甲骑摩托车的速度为40千米/小时,乙开汽车的速度为80千米/小时;
(2)当0≤t≤1时,设s=kt+b,
将(0,120),(1,0)代入,得:
$\left\{\begin{array}{l}{b=120}\\{k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-120}\\{b=120}\end{array}\right.$,
故此时s=-120t+120,
当s=100时,-120t+120=100,解得:t=$\frac{1}{6}$;
当1.5≤t≤3时,设s=mt+n,
将(1.5,60),(3,120)代入,得:
$\left\{\begin{array}{l}{1.5m+n=60}\\{3m+n=120}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=40}\\{n=0}\end{array}\right.$,
故此时s=40t,
当s=100时,40t=100,解得:t=2.5;
答:甲出发后$\frac{1}{6}$或2.5小时甲、乙两人相距100千米.
点评 本题主要考查一次函数的实际应用能力,根据题意弄清图象的实际意义是解题的基础和关键.

练习册系列答案
相关题目
1.在一个不透明的袋中装有除颜色外其余都相同的3个小球,其中一个白球、两个红球.如果一次从袋中摸出两个球,那么摸出的两个球都是红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
18.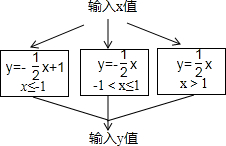 根据如图所示的程序计算函数值,若输入的x值为$-\frac{3}{2}$,则输出的结果y应为( )
根据如图所示的程序计算函数值,若输入的x值为$-\frac{3}{2}$,则输出的结果y应为( )
 根据如图所示的程序计算函数值,若输入的x值为$-\frac{3}{2}$,则输出的结果y应为( )
根据如图所示的程序计算函数值,若输入的x值为$-\frac{3}{2}$,则输出的结果y应为( )| A. | $\frac{7}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{9}{2}$ |

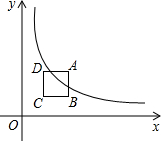 在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3.
在平面直角坐标系的第一象限内,边长为l的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a).如图,若曲线y=$\frac{4}{x}$(x>0)与此正方形的边有交点,则a的取值范围是2≤a≤3. 如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°.求证:AC=BD.
如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,又∠BED=90°.求证:AC=BD.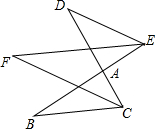 如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F
如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F