题目内容
11．
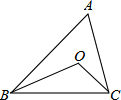已知：如图：△ABC中，∠B、∠C的角平分线交于点O，若∠A=60°，则∠BOC=120°．
分析 先根据三角形内角和定理求出∠ABC+∠ACB的度数，再由角平分线的性质得出∠OBC+∠OCB的度数，由三角形内角和定理即可得出结论．
解答 解：∵在△ABC中，∠A=60°，
∴∠ABC+∠ACB=180°-60°=120°，
∵∠ABC和∠ACB的平分线交于O点，
∴∠OBC+∠OCB=$\frac{1}{2}$（∠ABC+∠ACB）=$\frac{1}{2}$×120°=60°，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-60°=120°．
故答案为：120°
点评 本题考查的是三角形内角和定理，角平分线的性质，熟知三角形的内角和等于180°是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．在一个不透明的袋中装有除颜色外其余都相同的3个小球，其中一个白球、两个红球．如果一次从袋中摸出两个球，那么摸出的两个球都是红球的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
2．下列命题中，正确的个数是（ ）
①若三条线段的比为1：1：$\sqrt{2}$，则它们组成一个等腰直角三角形；
②两条对角线相等的平行四边形是矩形；
③对角线互相垂直的四边形是菱形；
④有两个角相等的平行四边形是矩形；
⑤一条直线与矩形的一组对边相交，必分矩形为两个直角梯形．
①若三条线段的比为1：1：$\sqrt{2}$，则它们组成一个等腰直角三角形；
②两条对角线相等的平行四边形是矩形；
③对角线互相垂直的四边形是菱形；
④有两个角相等的平行四边形是矩形；
⑤一条直线与矩形的一组对边相交，必分矩形为两个直角梯形．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
如图，在平行四边形ABCD中，以AC为斜边作Rt△ACE，又∠BED=90°．求证：AC=BD．
6．下列每组数分别是三根小木棒的长度（cm），用它们能摆成三角形的是（ ）
| A． | 3 4 9 | B． | 2 3 5 | C． | 5 12 13 | D． | 5 5 11 |
已知：如图，在△ABC中，AB=AD=DC，∠BAD=30°；试求∠B和∠C的度数．
3．点A（-1，y1），B（2，y2）在双曲线$y=\frac{1}{x}$上，则y1，y2的大小关系是（ ）
| A． | y1＜y2 | B． | y1=y2 | C． | y1＞y2 | D． | 不能确定 |
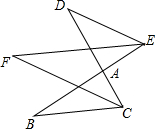如图，BE，CD相交于点A，∠DEA、∠BCA的平分线相交于F