题目内容
15.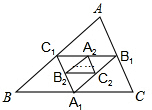 如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的面积是32,△A1B1C1的面积是S1,△A2B2C2的面积是S2,…,则△A4B4C4的面积S4=$\frac{1}{8}$.
如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的面积是32,△A1B1C1的面积是S1,△A2B2C2的面积是S2,…,则△A4B4C4的面积S4=$\frac{1}{8}$.
分析 根据三角形的中位线求出BC=2B1C1,AB=2A1B1,AC=2A1C1,求出$\frac{{A}_{1}{B}_{1}}{AB}$=$\frac{{B}_{1}{C}_{1}}{BC}$=$\frac{{A}_{1}{C}_{1}}{AC}$=$\frac{1}{2}$,根据相似三角形的判定得出△ABC∞△A1B1C1,根据相似三角形的性质得出$\frac{{S}_{△{A}_{1}{B}_{1}{C}_{1}}}{{S}_{△ABC}}$=$\frac{1}{4}$,推出S1=$\frac{1}{4}$S△ABC,得出规律,即可求出答案.
解答 解:∵A1、B1、C1分别是BC、AC、AB的中点,
∴BC=2B1C1,AB=2A1B1,AC=2A1C1,
∴$\frac{{A}_{1}{B}_{1}}{AB}$=$\frac{{B}_{1}{C}_{1}}{BC}$=$\frac{{A}_{1}{C}_{1}}{AC}$=$\frac{1}{2}$,
∴△ABC∞△A1B1C1,
∴$\frac{{S}_{△{A}_{1}{B}_{1}{C}_{1}}}{{S}_{△ABC}}$=($\frac{1}{2}$)2=$\frac{1}{4}$,
∵△ABC的面积是32,△A1B1C1的面积是S1,
∴S1=$\frac{1}{4}$S△ABC=$\frac{1}{4}$×32=8,
同理S2=$\frac{1}{4}$S1=2,
S3=$\frac{1}{4}$S2=$\frac{1}{2}$,
S4=$\frac{1}{4}$S3=$\frac{1}{8}$.
故答案为:$\frac{1}{8}$.
点评 本题考查了三角形的中位线,相似三角形的性质和判定的应用,能得出规律是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案| A. | 3 4 9 | B. | 2 3 5 | C. | 5 12 13 | D. | 5 5 11 |
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |

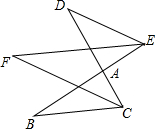 如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F
如图,BE,CD相交于点A,∠DEA、∠BCA的平分线相交于F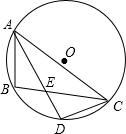 如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.
如图,AB,AC是⊙O弦,∠BAC的角平分线交⊙O于点D,AD与BC交于点E,若DE=2cm,AE=8cm,则DC=2$\sqrt{5}$cm.