题目内容
8．已知反比例函数$y=\frac{6}{x}$，当1＜x＜3时，y的取值范围是2＜y＜6．分析 利用反比例函数的性质，由x的取值范围并结合反比例函数的图象解答即可．
解答 解：∵k=6＞0，
∴在每个象限内y随x的增大而减小，
又∵当x=1时，y=6，
当x=3时，y=2，
∴当1＜x＜3时，2＜y＜6．
故答案为：2＜y＜6．
点评 本题主要考查反比例函数的性质，当k＞0时，在每一个象限内，y随x的增大而减小；当k＜0时，在每一个象限，y随x的增大而增大．
练习册系列答案
相关题目
18．
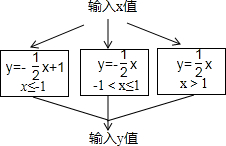根据如图所示的程序计算函数值，若输入的x值为$-\frac{3}{2}$，则输出的结果y应为（ ）
根据如图所示的程序计算函数值，若输入的x值为$-\frac{3}{2}$，则输出的结果y应为（ ）| A． | $\frac{7}{4}$ | B． | $-\frac{3}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{9}{2}$ |
如图，在平行四边形ABCD中，以AC为斜边作Rt△ACE，又∠BED=90°．求证：AC=BD．
已知：如图，在△ABC中，AB=AD=DC，∠BAD=30°；试求∠B和∠C的度数．
3．点A（-1，y1），B（2，y2）在双曲线$y=\frac{1}{x}$上，则y1，y2的大小关系是（ ）
| A． | y1＜y2 | B． | y1=y2 | C． | y1＞y2 | D． | 不能确定 |
如图，已知△ABC的三个顶点均在正方形网格的格点上，则cosA的值为$\frac{2\sqrt{5}}{5}$．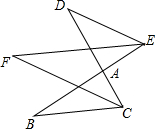
如图，BE，CD相交于点A，∠DEA、∠BCA的平分线相交于F