题目内容
 在△ABC中,∠C=90°,G是内心,BG与AC交于D,过D作DE∥AG与BC交BC于E,直线EG与AB交于F,求证:DF⊥AG.
在△ABC中,∠C=90°,G是内心,BG与AC交于D,过D作DE∥AG与BC交BC于E,直线EG与AB交于F,求证:DF⊥AG.考点:四点共圆,平行线的性质,线段垂直平分线的性质,等腰三角形的性质,圆周角定理,圆内接四边形的性质,三角形的内切圆与内心
专题:证明题
分析:连接CG,易得∠AGD=∠BAG+∠ABG=45°,从而可得∠AGD=∠GDE=∠GCE=45°,由此可得G、D、C、E四点共圆,根据圆内接四边形的性质可得∠BGE=∠DCE=90°,根据圆周角定理可得∠GED=∠GCD=45°,易证∠BFG=∠BEG,则有BE=BF,根据等腰三角形的性质可得FG=GE,然后根据垂直平分线的性质可得DE=DF,从而可得∠EDF=90°,根据AG∥DE就可证到DF⊥AG.
解答:证明:连接CG,如图.
∵G是△ABC内心,
∴∠ACG=∠GCB=
∠ACB=45°,∠BAG=
∠CAB,∠ABG=
∠ABC.
∵∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠BAG+∠ABG=
∠CAB+
∠ABC=45°,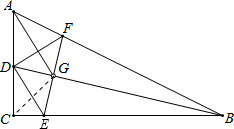
∴∠AGD=∠BAG+∠ABG=45°.
∵DE∥AG,
∴∠GDE=∠AGD=45°,
∴∠GDE=∠GCE=45°,
∴G、D、C、E四点共圆,
∴∠GED=∠GCD=45°,∠BGE=∠DCE=90°,
∴∠BFG=90°-∠FBG=90°-∠EBG=∠BEG,
∴BE=BF.
又∵BG⊥EF,
∴FG=GE.
∵BG⊥EF,FG=GE,
∴BD垂直平分EF,
∴DE=DF,
∴∠DFE=∠DEF=45°,
∴∠FDE=90°,即DF⊥DE,
∵AG∥DE,
∴DF⊥AG.
∵G是△ABC内心,
∴∠ACG=∠GCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ACB=90°,
∴∠CAB+∠ABC=90°,
∴∠BAG+∠ABG=
| 1 |
| 2 |
| 1 |
| 2 |

∴∠AGD=∠BAG+∠ABG=45°.
∵DE∥AG,
∴∠GDE=∠AGD=45°,
∴∠GDE=∠GCE=45°,
∴G、D、C、E四点共圆,
∴∠GED=∠GCD=45°,∠BGE=∠DCE=90°,
∴∠BFG=90°-∠FBG=90°-∠EBG=∠BEG,
∴BE=BF.
又∵BG⊥EF,
∴FG=GE.
∵BG⊥EF,FG=GE,
∴BD垂直平分EF,
∴DE=DF,
∴∠DFE=∠DEF=45°,
∴∠FDE=90°,即DF⊥DE,
∵AG∥DE,
∴DF⊥AG.
点评:本题主要考查了四点共圆的判定、三角形的内心、平行线的性质、圆内接四边形的性质、圆周角定理、垂直平分线的性质、等腰三角形的性质等知识,综合性强,证到G、D、C、E四点共圆是解决本题的关键.

练习册系列答案
相关题目
无论x为何实数,下列各式总有意义的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
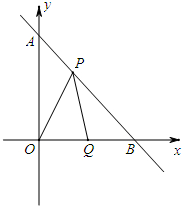 如图,直线y=-x+1与x轴,y轴分别交于A,B两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,交x轴于点Q.
如图,直线y=-x+1与x轴,y轴分别交于A,B两点,动点P在线段AB上移动,以P为顶点作∠OPQ=45°,交x轴于点Q.