题目内容
1.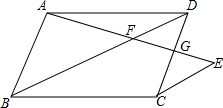 已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.
已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.(1)求证:CE∥BD;
(2)当点G为CD中点时,求证:BD=3CE.
分析 (1)连接AC交BD于O,由平行四边形的性质得出AO=CO,证出OF是△ACE的中位线,由三角形中位线定理得出OF∥CE即可.
(2)由平行四边形的性质得出AB=CD,AB∥CD,OB=OD,证出DG=$\frac{1}{2}$CD=$\frac{1}{2}$AB,由平行线的性质得出△FAB∽△FDG,得出比例式$\frac{DF}{BF}$=$\frac{DG}{AB}$=$\frac{1}{2}$,∴$\frac{OD-OF}{OB+OF}$=$\frac{1}{2}$,得出BD=6OF,由(1)得CE=2OF,即可得出结论.
解答 证明:(1)连接AC交BD于O,如图所示: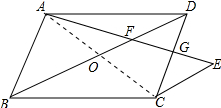
∵ABCD是平行四边形,
∴AO=CO,
∵AF=EF,
∴OF是△ACE的中位线,
∴OF∥CE,
即CE∥BD;
(2)∵ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,
∵G为CD的中点,
∴DG=$\frac{1}{2}$CD=$\frac{1}{2}$AB,
∵AB∥CD,
∴△FAB∽△FDG,
∴$\frac{DF}{BF}$=$\frac{DG}{AB}$=$\frac{1}{2}$,
∴$\frac{OD-OF}{OB+OF}$=$\frac{1}{2}$,
∴2(OD-OF)=OD+OF,
∴OD=3OF,
∴BD=6OF,
由(1)得CE=2OF,
∴BD=3CE.
点评 本题考查了平行四边形的性质、三角形中位线定理、相似三角形的判定与性质等知识;熟练掌握平行四边形的性质,证明三角形相似得出比例式是解决问题(2)的关键.

练习册系列答案
相关题目
16.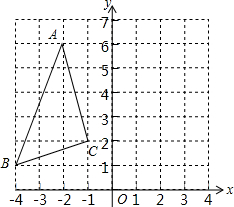 如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
 如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )
如图,如果将△ABC先向右平移1个单位长度,再绕原点O顺时针旋转90°,得到△A1B1C1,那么点A的对应点A1的坐标为( )| A. | (1,3) | B. | (2,0) | C. | (6,1) | D. | (6,2) |
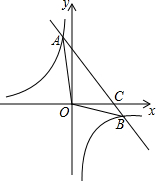 如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C
如图,已知一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,m)和点B(4,-2),与x轴交于点C 如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G.
如图,在?ABCD中,AB=8,BC=6,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将?ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点H,点D的对应点为点G. 如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$).
如图,已知A,B两村庄在平面直角坐标系中的坐标分别为(3,1),(5,5),若长途客车沿y轴行驶到P处时,与A,B两村庄的距离之和最小,则点P的坐标为(0,$\frac{5}{2}$). 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B的对应点E落在坐标平面内,当△ADE是等腰直角三角形时,点E的坐标为(0,1).