题目内容
11.计算:$\sqrt{(x-\frac{1}{x})^{2}+4}$-$\sqrt{(x+\frac{1}{x})^{2}-4}$(0<x<1)分析 先把被开方数化为完全平方式的形式,再去根号,合并同类项即可.
解答 解:原式=$\sqrt{(x+\frac{1}{x})^{2}}$-$\sqrt{{(x-\frac{1}{x})}^{2}}$
=x+$\frac{1}{x}$-($\frac{1}{x}$-x)
=x+$\frac{1}{x}$-$\frac{1}{x}$+x
=2x.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
相关题目
1.在解分式方程$\frac{1}{x-1}$+$\frac{x}{x-1}$=2时,我们第一步通常是去分母,即方程两边同乘以最简公分母(x-1),把分式方程变形为整式方程求解.解决这个问题的方法用到的数学思想是( )
| A. | 数形结合 | B. | 转化思想 | C. | 模型思想 | D. | 特殊到一般 |
2.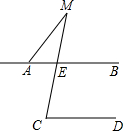 如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
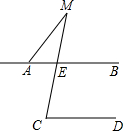 如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )
如图,AB∥CD,∠A=142°,∠C=80°,那么∠M=( )| A. | 52° | B. | 42° | C. | 10° | D. | 40° |
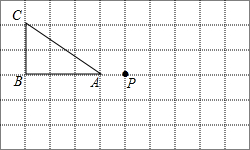 如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′.
如图,将△ABC绕点O顺时针旋转180°后得到△A′B′C′.请画出旋转后的△A′B′C′.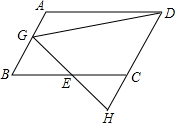 如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.
如图,在?ABCD中,E为BC中点,过点E作EG⊥AB于G,连结DG,延长DC,交GE的延长线于点H.已知BC=10,∠GDH=45°,DG=8$\sqrt{2}$.求CD的长.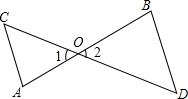 如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.
如图,AB和CD相交于点O,∠C=∠1,∠D=∠2,求证:∠A=∠B.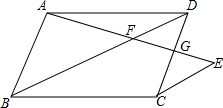 已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.
已知:如图,在?ABCD中,AE与对角线BD相交于点F,EF=AF.