题目内容
19.如图,已知AB∥CD,请分别判断下面四个图形中∠APC、∠PAB、∠PCD之间的关系.(1)写出相应的四个结论;
(2)请证明你所得的第③个图形的结论.

分析 分别过点P作PE∥AB,然后根据平行线的性质解答即可.
解答 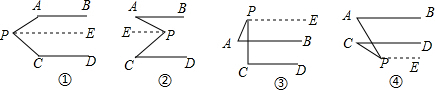 (1)解:①∠APC+∠PAB+∠PCD=360°,
(1)解:①∠APC+∠PAB+∠PCD=360°,
②∠APC=∠PAB+∠PCD,
③∠APC=∠PCD-∠PAB,
④∠APC=∠PAB-∠PCD;
(2)证明:如图,过点P作PE∥AB,
∴∠APE=180°-∠PAB,
∵AB∥CD,
∴PE∥CD,
∴∠CPE=180°-∠PCD,
∴∠APC=∠APE-∠CPE=(180°-∠PAB)-(180°-∠PCD)=∠PCD-∠PAB.
点评 本题考查了平行线的性质,此类题目,难点在于过拐点作平行线.

练习册系列答案
相关题目
14.平行四边形ABCD中,∠A比∠B大40°,则∠D的度数为( )
| A. | 60° | B. | 70° | C. | 100° | D. | 110° |
 如图,在三角形ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°.
如图,在三角形ABC中,过点C作CD∥AB,且∠1=70°,点E是AC边上的一点,且∠EFB=130°,∠2=20°.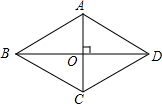 如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可)
如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可) 已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.
已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.