题目内容
9. 已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.
已知:如图,在四边形ABCD中,P、Q、M、N分别是AD、BC、BD、AC的中点.(1)求证:PQ、MN互相平分;
(2)当四边形ABCD的边满足条件:AB=CD时,PQ⊥MN.(不必证明)
分析 (1)连接MP、NP、MQ、NQ,根据三角形中位线定理得到PM=$\frac{1}{2}$AB,PM∥AB,NQ=$\frac{1}{2}$AB,NQ∥AB,根据平行四边形的判定定理证明四边形PMQN是平行四边形,根据平行四边形的性质定理证明结论;
(2)根据菱形的判定定理和性质定理解答即可.
解答 (1)证明:连接MP、NP、MQ、NQ,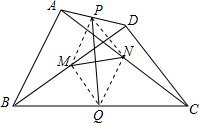
∵P、M分别是AD、BD的中点,
∴PM=$\frac{1}{2}$AB,PM∥AB,
同理NQ=$\frac{1}{2}$AB,NQ∥AB,
∴PM∥NQ,PM=NQ,
∴四边形PMQN是平行四边形,
∴PQ、MN互相平分;
(2)AB=CD,
∵PM=$\frac{1}{2}$AB,PN=$\frac{1}{2}$CD,
当AB=CD时,PM=PN,
则平行四边形PMQN是菱形,
∴PQ⊥MN.
点评 本题考查的是中点四边形的证明,掌握三角形中位线定理、平行四边形的判定定理、菱形的判定定理和性质定理是解题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.下列说法不正确的是( )
| A. | 0.4的算术平方根是0.2 | B. | -9是81的一个平方根 | ||
| C. | -27的立方根是-3 | D. | 1-$\sqrt{2}$的相反数是$\sqrt{2}$-1 |
14.在x=1,y=5x,x2=0,xy=2这四个方程中,是一元一次方程的是( )
| A. | x=1 | B. | y=5x | C. | x2=0 | D. | xy=2 |
19.下列一元二次方程有两个相等实数根的是( )
| A. | x2+3=0 | B. | (x+1)2=0 | C. | x2+2x=0 | D. | (x+3)(x-1)=0 |

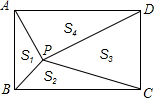 如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论的序号是②④.
如图所示,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论的序号是②④. 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作EF⊥AC分别交AD、BC于F、E.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作EF⊥AC分别交AD、BC于F、E.