题目内容
11.已知关于x,y的方程组$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$,其中-3≤a≤1,给出下列结论:①当a=1时,方程组的解也是方程x+y=4-a的解;②当a=-2时,x、y的值互为相反数;③$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$是方程组的解,其中正确的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 把a=1代入方程组,可求得方程组的解,再代入方程x+y=4-a进行判断,可判断①;把x=-2代入方程组,可求得方程组的解,可判断②;把$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$代入方程可求得a的值为2,可判断③;可得出答案.
解答 解:当a=1时,原方程组为$\left\{\begin{array}{l}{x+3y=3}\\{x-y=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$代入方程x+y=3成立,即$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$也是方程x+y=4-a的解,
故①正确;
当a=-2时,原方程组为$\left\{\begin{array}{l}{x+3y=6}\\{x-y=-6}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-3}\\{y=3}\end{array}\right.$,
故②正确;
当$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$时,代入方程组可求得a=2,
∴即只有当a=2时,方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=-1}\end{array}\right.$,
故③不正确;
综上可知正确的为①②.
故选A.
点评 本题主要考查二元一次方程解的定义和解二元一次方程组,根据条件分别求得方程组的解是解题的关键.

| A. | 3x-6=x | B. | 3x=2y | C. | 2x+$\frac{3}{y}$=1 | D. | 2x-3y=xy |
| A. | 4 | B. | 49 | C. | 4或49 | D. | 1或49 |
| A. | (x+2)2=10 | B. | (x-2)2=10 | C. | (x+2)2=2 | D. | (x-2)2=2 |
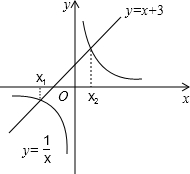 如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )
如图,方程x2+3x=1的根可看作是函数y=x+3的图象与函数y=$\frac{1}{x}$的图象交点的横坐标.类似地,利用这种图象法,可以确定方程x2+2x-1=0的实数根x0所在的范围是( )| A. | 0<x0<$\frac{1}{4}$ | B. | $\frac{1}{4}$<x0<$\frac{1}{3}$ | C. | $\frac{1}{3}$<x0<$\frac{1}{2}$ | D. | $\frac{1}{2}$<x0<1 |
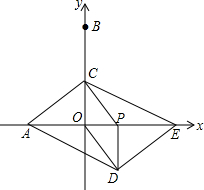 如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.
如图,在平面直角坐标系中,点A,B的坐标分别为(-3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造平行四边形PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.