题目内容
11.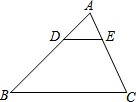 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{3}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
分析 根据$\frac{AD}{AB}$=$\frac{1}{3}$,求得$\frac{AD}{BD}$=$\frac{1}{2}$,由DE∥BC,根据平行线分线段成比例定理得到$\frac{AE}{CE}=\frac{AD}{BD}$=$\frac{1}{2}$,根据相似三角形的性质得到结论.
解答 解:∵$\frac{AD}{AB}$=$\frac{1}{3}$,
∴$\frac{AD}{BD}$=$\frac{1}{2}$,
∵DE∥BC,
∴$\frac{AE}{CE}=\frac{AD}{BD}$=$\frac{1}{2}$,△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{AD}{AB}=\frac{1}{3}$,$\frac{△ADE的周长}{△ABC的周长}$=$\frac{AD}{AB}$=$\frac{1}{3}$,$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{AD}{AB}$)2=$\frac{1}{9}$,
故A,B,D错误,
故选C.
点评 本题主要考查了相似三角形的判定和性质,掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
20. 如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )
如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )
 如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )
如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{13}$ |
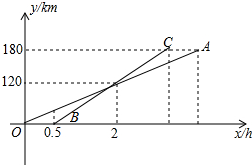 “十一”黄金周期间,某校八年级一班和八年级二班的学生沿同一条路线去某旅游区旅游,图中直线OA,BC分别表示一班和二班行驶路程y和所用时间x之间的函数图象.请你根据图中题中的信息,解答下列问题:
“十一”黄金周期间,某校八年级一班和八年级二班的学生沿同一条路线去某旅游区旅游,图中直线OA,BC分别表示一班和二班行驶路程y和所用时间x之间的函数图象.请你根据图中题中的信息,解答下列问题: