题目内容
19.星期天,小明步行到6km远的学校去参加活动,从早晨7时出发,要在9时前到达,如果他每小时走xkm,可以得到的不等式是什么?根据这个不等式,判断x的取值范围.分析 要求实际每小时行驶多少千米,应求出路程和实际所用的时间.根据题意,路程为6千米,时间为最多2小时,进而得出答案.
解答 解:设他每小时要走x km,则可列不等式为:
2x≥6,
解得:x≥3.
点评 此题运用了由实际问题抽象出一元一次不等式,利用关系式:速度×时间=路程得出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | |-$\frac{1}{7}$| | D. | $\sqrt{2}$ |
7.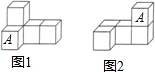 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )| A. | 主视图 | B. | 主视图和左视图 | C. | 主视图和俯视图 | D. | 左视图和俯视图 |
11.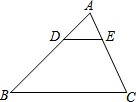 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{3}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
8.在方程(k2-4)x2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k值为( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 以上答案都不对 |
 如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.
如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.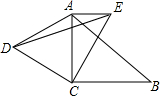 如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.
如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.
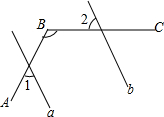 如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2=70°.
如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2=70°.