题目内容
2.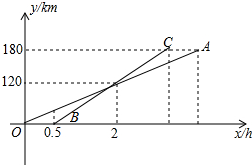 “十一”黄金周期间,某校八年级一班和八年级二班的学生沿同一条路线去某旅游区旅游,图中直线OA,BC分别表示一班和二班行驶路程y和所用时间x之间的函数图象.请你根据图中题中的信息,解答下列问题:
“十一”黄金周期间,某校八年级一班和八年级二班的学生沿同一条路线去某旅游区旅游,图中直线OA,BC分别表示一班和二班行驶路程y和所用时间x之间的函数图象.请你根据图中题中的信息,解答下列问题:(1)哪个班出发的早?早多长时间?
(2)从出发地到目的地所走的路程是多少千米?
(3)八年级二班从出发到与一班相遇总共用了多少小时?
(4)一班的行驶速度是多少?二班呢?
(5)一班从出发到到达目的地总共用了多少小时?
(6)求出一班、二班的行驶路程y(千米)和时间x(小时) 之间的函数关系式.
分析 (1)根据图象得出信息即可;
(2)根据图象即可直接得到信息;
(3)根据图象可得利用相遇的时刻2小时减去0.5小时即可求得;
(4)利用速度公式即可直接求解;
(5)利用总路程除以速度即可求解;
(6)首先求得A和C的坐标,然后利用待定系数法即可求解.
解答 解:(1)八年级一班出发早,早0.5小时;
(2)从出发地道目的地所走的路程是180km;
(3)八年级二班从出发到与一班相遇总共用2-0.5=1.5(小时);
(4)一班的速度是$\frac{120}{2}$=60(km/h),二班的速度是$\frac{120}{1.5}$=80km/h;
(5)一班从出发到到达目的地总共用了$\frac{180}{60}$=3(h);
(6)根据(4)可得A的坐标是(3,180).
设AC的解析式是y=kx,
根据题意得:3k=180,
解得:k=60,
则一班的路程y与时间x的函数关系是y=-60x;
二班从出发到到达目的地总共用$\frac{180}{80}$=$\frac{9}{4}$(小时),则C的坐标是($\frac{11}{4}$,180).
设BC的解析式是y=mx+n,
则$\left\{\begin{array}{l}{0.5m+n=0}\\{\frac{11}{4}m+n=180}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=80}\\{n=-40}\end{array}\right.$,
则二班的路程和时间的函数关系式是y=80x-40.
点评 本题考查了一次函数的图象,以及待定系数法求函数的解析式,读懂图象是解题的关键.

练习册系列答案
相关题目
10.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | |-$\frac{1}{7}$| | D. | $\sqrt{2}$ |
17. 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
7.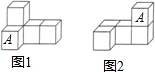 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )| A. | 主视图 | B. | 主视图和左视图 | C. | 主视图和俯视图 | D. | 左视图和俯视图 |
11.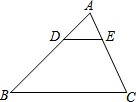 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{3}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
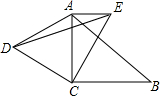 如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.
如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.