题目内容
20. 如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )
如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是$\widehat{CF}$的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{13}$ |
分析 根据垂径定理求出CF=2CE,根据切线的性质求出∠OCD,求出∠COE的度数,解直角三角形求出CE即可.
解答 解:连接OC,
∵点B是$\widehat{CF}$的中点,AB为⊙O的直径,
∴CE=EF,CF⊥AB,
∴∠CEO=90°,
∵DC切⊙O于C,
∴∠OCD=90°,
∵OB=BD=OC=2,
∴∠D=30°,
∴∠COE=60°,
∴CE=OC×sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴CF=2CE=2$\sqrt{3}$,
故选B.
点评 本题考查了切线的性质,垂径定理,解直角三角形的应用,能求出CF=2CE和∠COE的度数是解此题的关键,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | |-$\frac{1}{7}$| | D. | $\sqrt{2}$ |
11.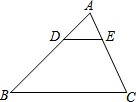 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{AB}$=$\frac{1}{3}$,则下列结论中正确的是( )| A. | $\frac{AE}{EC}$=$\frac{1}{3}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |
8.在方程(k2-4)x2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k值为( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 以上答案都不对 |
5.2015年羊年除夕夜,中央电视台春晚送红包活动中,送出微信红包约120 000 000个,将120 000 000用科学记数法表示应为( )
| A. | 0.12×109 | B. | 1.2×107 | C. | 1.2×108 | D. | 12×107 |
12.下列四个不等式:①-$\frac{2}{3}$<-0.67;②-$\frac{1}{4}$>-0.24;③-$\frac{5}{6}$>-$\frac{4}{5}$;④-$\frac{3}{11}$<$-\frac{1}{4}$.其中正确的是( )
| A. | ②④ | B. | ①③ | C. | ②③ | D. | ④ |
10.设a是方程x2+2x-2=0的一个实数根,则2a2+4a+2016的值为( )
| A. | 2016 | B. | 2018 | C. | 2020 | D. | 2021 |
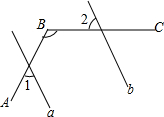 如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2=70°.
如图所示,直线a平移后得到直线b,∠1=60°,∠B=130°,则∠2=70°.