题目内容

在等边△ABC中，点D、E分别在AB、AC边上，且DE∥BC．如果BC=8cm，AD：DB=1：3，那么△ADE的周长等于
 
cm．
考点：平行线分线段成比例,等边三角形的性质
专题：计算题
分析：先证明△ADE为等边三角形，再根据平行线分线段成比例定理，由DE∥BC得到
DE
BC
=
AD
AB
，然后利用比例性质计算出DE，从而得到△ADE的周长．
解答：解：如图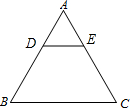，∵△ABC为等边三角形，
∴∠A=∠B=∠C=60°，
∵DE∥BC，
∴∠ADE=∠B=60°，∠AED=∠C=60°，
∴△ADE为等边三角形，
∴AD=DE=AE，
∵DE∥BC，
∴
DE
BC
=
AD
AB
，
∵AD：DB=1：3，
∴
DE
8
=
1
4
，解得DE=2，
∴△ADE的周长=2+2+2=6（cm）．
故答案为6．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；平行于三角形的一边，并且和其他两边（或两边的延长线）相交的直线，所截得的三角形的三边与原三角形的三边对应成比例．也考查了等边三角形的性质．
练习册系列答案
相关题目
如图，数轴上有两点A，B，点A表示的数为4，点B在点A的左侧，且AB=10，动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）．
（1）写出数轴上点B表示的数
 
，点P表示的数用含t的代数式表示：
 
．
（2）设点M是AP的中点，点N是PB的中点．点P在线段AB上运动过程中，线段MN的长度是否发生变化？若变化，请说出理由；若不变，求线段MN的长度．
（3）动点R从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P，R同时出发，问点P运动多少秒与点R距离为2个单位长度．
如图，AE是位于公路边的电线杆，高为12m，为了使拉线CDE不影响汽车的正常行驶，电力部门在公路的另一边竖立了一根为6m的水泥撑杆BD，用于撑起电线．已知两根杆子之间的距离为8m，电线CD与水平线AC的夹角为60°．求电线CDE的总长L（A、B、C三点在同一直线上，电线杆、水泥杆的大小忽略不计）．
如图所示，点P是正六边形ABCDEF内一点，若△PAB，△PBC，△PCD，△PDE，△PEF，△PFA的面积依次为S1，S2，S3，S4，S5，S6，且S1-S2+S3=1，则S3+S6=
 
．
在雨地里放置一个无盖的容器，如果雨水均匀地落入容器，容器水面高度h与时间t的函数图象如图所示，那么这个容器的形状可能是（　　）
A、
B、
C、
D、
如图1、图2是正方形网格，并建立了直角坐标系，O为原点，每个小正方形的顶点叫做格点．
（1）请你在图1中，画出△ABC关于点O成中心对称的△A′B′C′．
（2）如图2，小明和小亮用这个正方形网格作概率的试验．小明在第二象限内选取三个点A1、A2、A3，小亮在第四象限内选取三个点B1、B2、B3，请你用列表或画树状图的方法计算，小明、小亮各选取一个点能关于某一格点成中心对称的概率是多少．
如图，在平面直角坐标系中，△ABC的三个顶点A（4，3），B（1，4），C（2，1）．
（1）将△ABC以点D（0，1）为旋转中心旋转180°，画出旋转后对应的△A1B1C1；平移△A1B1C1，若B1点的对应点B2的坐标为（5，-3），画出平移后对应的△A2B2C2；
（2）若将△A2B2C2绕某一点旋转可以得到△ABC，请直接写出旋转中心坐标；
（3）在y轴上有一点F，使得FA-FB的值最大，请直接写出点F的坐标．
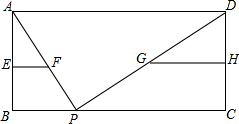如图，已知平行四边形ABCD中，AD=10cm，点P在边BC边上移动，点E、F、G、H分别是AB、AP、DP、DC的中点，请探索在移动过程中，EF+GH的值是否改变？若不变，请求EF+GH的值．
现有若干个三角形，在所有的内角中，有4个直角，5个钝角，27个锐角，则在这些三角形中锐角三角形的个数是（　　）
A、3B、4或5C、6或7D、8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网