题目内容
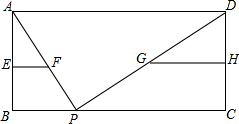 如图,已知平行四边形ABCD中,AD=10cm,点P在边BC边上移动,点E、F、G、H分别是AB、AP、DP、DC的中点,请探索在移动过程中,EF+GH的值是否改变?若不变,请求EF+GH的值.
如图,已知平行四边形ABCD中,AD=10cm,点P在边BC边上移动,点E、F、G、H分别是AB、AP、DP、DC的中点,请探索在移动过程中,EF+GH的值是否改变?若不变,请求EF+GH的值.考点:三角形中位线定理
专题:
分析:EF、GH分别是△ABP和△DPC的中位线,根据三角形的中位线定理即可求解.
解答:解:EF+GH的值不改变.
∵E、F分别是AB、AP的中点,即EF是△ABP的中位线,
∴EF=
BP.
同理,GH=
PC.
∴EF+GH=
(BP+PC)=
BC=
×10=5(cm).
∵E、F分别是AB、AP的中点,即EF是△ABP的中位线,
∴EF=
| 1 |
| 2 |
同理,GH=
| 1 |
| 2 |
∴EF+GH=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的中位线定理,理解定理是解题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知:等腰三角形两边长分别为9cm,5cm,则周长是( )
| A、19cm |
| B、23cm |
| C、19cm或23cm |
| D、不能确定 |
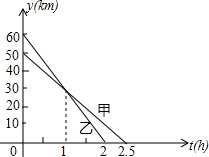 甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发
甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发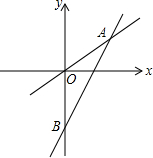 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.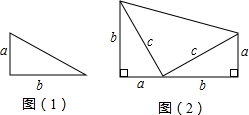
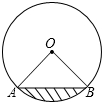 如图,水平放置的圆柱形排水管道的横截面半径是2
如图,水平放置的圆柱形排水管道的横截面半径是2