题目内容
 如图所示,点P是正六边形ABCDEF内一点,若△PAB,△PBC,△PCD,△PDE,△PEF,△PFA的面积依次为S1,S2,S3,S4,S5,S6,且S1-S2+S3=1,则S3+S6=
如图所示,点P是正六边形ABCDEF内一点,若△PAB,△PBC,△PCD,△PDE,△PEF,△PFA的面积依次为S1,S2,S3,S4,S5,S6,且S1-S2+S3=1,则S3+S6=考点:面积及等积变换
专题:
分析:由于点P在正六边形ABCDEF内任意位置时所对应的S3+S6的值都是某个确定的值,因此只需求出点P在正六边形ABCDEF中心时所对应的S3+S6的值就可解决问题.
解答:解:当点P在正六边形ABCDEF中心时,有S1=S2=S3=S4=S5=S6.
∵S1-S2+S3=1,
∴S3=1,
∴S6=1,
∴S3+S6=2.
故答案为2.
∵S1-S2+S3=1,
∴S3=1,
∴S6=1,
∴S3+S6=2.
故答案为2.
点评:考查了面积及等积变换,本题是一道填空题,在解决问题的过程中运用特殊化法,渗透了特殊与一般的辩证思想.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
下列运算中,可用平方差公式计算的是( )
| A、(x+y)(x+y) |
| B、(-x+y)(x-y) |
| C、(-x-y)(y-x) |
| D、(x+y)(-x-y) |
下列运算正确的是( )
| A、а2•а3=а6 |
| B、(-а2)3=-а6 |
| C、(аb)2=аb2 |
| D、а6÷а3=а2 |
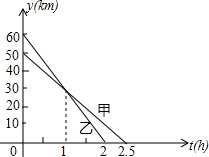 甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发
甲乙两人在一笔直的公路上,沿同一方向骑自行车同时出发前往A地,到A地后停止,他们距A地的路程ykm与甲行驶的时间x小时之间的关系如图所示,则出发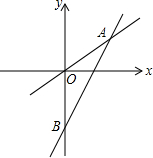 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.