题目内容
6.计算(1)3$\sqrt{5}$-$\sqrt{2}$+$\sqrt{5}$-4$\sqrt{2}$
(2)2$\sqrt{75}$-3$\sqrt{27}$+$\sqrt{12}$
(3)$\sqrt{72}$+$\sqrt{18}$-$\frac{3\sqrt{2}}{2}$
(4)2$\sqrt{\frac{2}{3}}$-3$\sqrt{\frac{3}{2}}$+$\sqrt{24}$.
分析 (1)直接合并同类二次根式进而得出即可;
(2)首先化简二次根式进而合并求出即可;
(3)首先化简二次根式进而合并求出即可;
(4)首先化简二次根式进而合并求出即可.
解答 解:(1)3$\sqrt{5}$-$\sqrt{2}$+$\sqrt{5}$-4$\sqrt{2}$=4$\sqrt{5}$-5$\sqrt{2}$;
(2)2$\sqrt{75}$-3$\sqrt{27}$+$\sqrt{12}$
=10$\sqrt{3}$-9$\sqrt{3}$+2$\sqrt{3}$
=3$\sqrt{3}$;
(3)$\sqrt{72}$+$\sqrt{18}$-$\frac{3\sqrt{2}}{2}$
=6$\sqrt{2}$+3$\sqrt{2}$-$\frac{3\sqrt{2}}{2}$
=$\frac{15\sqrt{2}}{2}$;
(4)2$\sqrt{\frac{2}{3}}$-3$\sqrt{\frac{3}{2}}$+$\sqrt{24}$
=$\frac{2\sqrt{6}}{3}$-$\frac{3\sqrt{6}}{2}$+2$\sqrt{6}$
=$\frac{3\sqrt{6}}{2}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
相关题目
11. 如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
 如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )
如图所示的两个几何体是由六个大小相同的小正方体组合而成的,则它们三视图中完全一致的是( )| A. | 主视图 | B. | 俯视图 | C. | 左视图 | D. | 三视图 |
5.直角三角形两直角边边长分别为6cm和8cm,则斜边的中线为( )
| A. | 10cm | B. | 3cm | C. | 4cm | D. | 5cm |
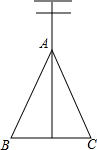 如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.
如图,电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定住了(AB=AC),但有工作人员说看上去有点倾斜,请你帮助工作人员测下电线杆是否倾斜,简要说明理由.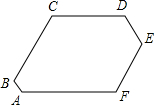 如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.
如图,已知六边形ABCDEF的每个内角都是120°且AB=1,DE=2,BC=CD=8,求此六边形的周长.