题目内容
18.已知关于x的多项式x3+x2+x+6=(x+2)(x2+ax+b),求a,b的值.分析 先计算(x+2)(x2+ax+b),然后将各个项的系数依次对应相等,求出a、b即可.
解答 解:(x+2)(x2+ax+b)=x3+ax2+bx+2x2+2ax+2b=x3+(a+2)x2+(b+2a)x+2b,
∵x3+x2+x+6=(x+2)(x2+ax+b),
∴$\left\{\begin{array}{l}{a+2=1}\\{2b=6}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
点评 本题考查了多项式乘以多项式,解题此类题目的基本思想是等式的左右两边各个项的系数相等,解题的关键是将等式的左右两边整理成相同的形式.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
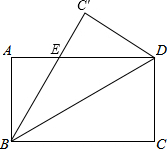 如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,B C′交AD于E,已知AB=3.
如图,把矩形ABCD沿对角线CD折叠,使点C落在C′处,B C′交AD于E,已知AB=3. 如图,在?ABCD中,BM平分∠ABC,且M为CD的中点,求证:AM平分∠DAB.
如图,在?ABCD中,BM平分∠ABC,且M为CD的中点,求证:AM平分∠DAB.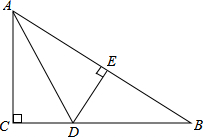 如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.