题目内容
14.已知关于x的一元二次方程x2-mx-2=0.(1)若m=1,方程的两个根为x1,x2,则x1+x2-x1x2=3;
(2)对于任意的实数m,判断方程的根的情况,并说明理由.
分析 (1)把m=1代入得出方程,再根据根与系数的关系得出x1+x2,x1x2,代入计算即可;
(2)根据根的判别式△进行判断即可.
解答 解:(1)∵m=1,
∴x2-x-2=0,
∴x1+x2=1,x1x2=-2,
∴x1+x2-x1x2=1+2=3,
故答案为3;
(2)∵a=1,b=-m,c=-2,
∴△=b2-4ac=m2+8,
∵m2≥0,
∴m2+8>0,
∴方程有两个不相等的实数根.
点评 本题考查了一元二次方程根与系数的关系以及根的判别式,掌握当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根是解题的关键.

练习册系列答案
相关题目
9.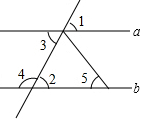 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )
 如图,在下列条件中,不能判定直线a与b平行的是( )
如图,在下列条件中,不能判定直线a与b平行的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠3+∠4=180° | D. | ∠3=∠5 |
7.某区的绿化覆盖率由如下统计数据:
如果以后的几年继续依此速度发展绿化.
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
| 年份 | 第1年年底 | 第2年年底 | 第3年年底 | 第4年年底 |
| 绿化覆盖率﹙%﹚ | 22.2 | 23.8 | 25.4 | 27.0 |
| 年份 | 第5年年底 | … | 第10年年底 | |
| 绿化覆盖率﹙%﹚ |
(1)观察此表格,第5年年底的绿化覆盖率为多少?
(2)探索规律,问第10年年底的绿化覆盖率为多少?第n年年底的绿化覆盖率为多少?﹙n≤35的正整数﹚
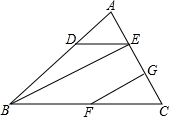 完成下面的证明:
完成下面的证明: