题目内容
5.如图(1)所示,已知AB=AC,D为∠BAC的角平分线上面的一点,连接BD、CD;如图(2)已知AB=AC,D、E、F为∠BAC的角平分线上面的三点,连接BD、CD、BE、CE、BF、CF;…,依次规律,第N个图形中有全等三角形的对数是$\frac{1}{2}$n(n+1).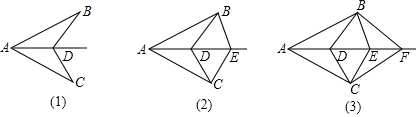
分析 根据图形得出当有1点D时,有1对全等三角形;当有2点D、E时,有3对全等三角形;当有3点D、E、F时,有6对全等三角形;根据以上结果得出当有n个点时,可求得有$\frac{1}{2}$n(n+1)对全等三角形.
解答 解:当有1个点:D时,有1对全等三角形;
当有2个点:D、E时,有3对全等三角形;
当有3个点:D、E、F时,有6对全等三角形;
当有4点时,有10个全等三角形;
…
当有n个点时,图中有$\frac{1}{2}$n(n+1)对全等三角形,
故答案为:$\frac{1}{2}$n(n+1).
点评 本题考查了对全等三角形的应用,关键是根据已知图形得出规律.

练习册系列答案
相关题目
16.一组数据的最大值是97,最小值是76,若组距为4,则可分为几组( )
| A. | 4组 | B. | 5组 | C. | 6组 | D. | 7组 |
10.某商场招聘员工一名,现有甲、乙两人竞聘,通过计算机、语言和商品知识三项测试,他们各自成绩(百分制)如下表所示
若商场需要招聘负责将商品拆装上架的人员,对计算机、语言和商品知识分别赋权2,3,5计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
| 应试者 | 计算机 | 语言 | 商品知识 |
| 甲 | 70 | 50 | 80 |
| 乙 | 90 | 75 | 45 |
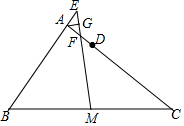 如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.
如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连结MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.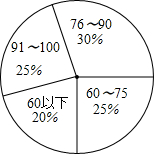 某校对八年级300名学生数学考试成绩作一次调查(得分均为整数)在某范围内的得分率如图所示,则在76-90这一分数段中的人数为( )
某校对八年级300名学生数学考试成绩作一次调查(得分均为整数)在某范围内的得分率如图所示,则在76-90这一分数段中的人数为( )