题目内容
14.我们知道:一个整数的个位数是偶数,则它一定能被2整除;一个整数的各位数字之和能被3整除,则它一定能被3整除.若一个整数既能被2整除又能被3整除,那么这个整数一定能被6整除.数字6象征顺利、吉祥,我们规定,能被6整除的四位正整数$\overline{abcd}$(千位数字为a,百位败字为b,十位数字为c,个位数字为d)是“吉样数”,请解答下面几个问题:(1)已知$\overline{785x}$是“吉样数”,则x=4.
(2)若正整数$\overline{abcd}$是“吉样数”,试说明:d+4(a+b+c)能被2整除.
(3)小明完成第(2)问后认为:四位正整数$\overline{abcd}$是“吉样数”,邯么d+4(a+b+c)也是“吉祥数字”.你认为他说得对吗?请说明理由.
分析 (1)根据“吉样数”的定义,由既能被2整除又能被3整除的数的特征求解即可;
(2)根据“吉样数”的定义,可得d是偶数,根据偶数的定义可知4(a+b+c)是偶数,从而求解;
(3)d+4(a+b+c)=a+b+c+d+3(a+b+c),通过证明“吉样数”的定义得出a+b+c+d能被3整除,结合(2)即可求解.
解答 解:(1)∵7+8+5=20,$\overline{785x}$是“吉样数”,
∴$\overline{785x}$中x只能为4;
(2)∵正整数$\overline{abcd}$是“吉样数”,
∴d是偶数,
∵4(a+b+c)是偶数,
∴d+4(a+b+c)是偶数,
∴d+4(a+b+c)能被2整除;
(3)对,
由(2)知d+4(a+b+c)能被2整除,
∵四位正整数$\overline{abcd}$是“吉样数”,
∴a+b+c+d能被3整除,
即a+b+c+d=3x,x为正整数,
∴d+4(a+b+c)
=a+b+c+d+3(a+b+c)
=3x+3(a+b+c)
=3(a+b+c+x),
∴d+4(a+b+c)能被3整除.
综上所述,d+4(a+b+c)是“吉祥数字”.
点评 考查了因式分解的应用,解题的关键是理解阅读材料的内容,以及理解“吉样数”的定义.

练习册系列答案
相关题目
14.下列计算,正确的是( )
| A. | a2-a=a | B. | a2•a3=a6 | C. | a9÷a3=a3 | D. | (a3)2=a6 |
6.已知二次函数y=x2-(m+1)x-5m(m为常数).在-1≤x≤3的范围内至少有一个x的值使y≥2,则m的取值范围是( )
| A. | m≤0 | B. | 0≤m≤$\frac{1}{2}$ | C. | m≤$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
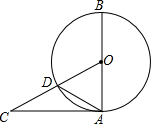 如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=120°.
如图,AB是⊙O的直径,AC与⊙O相切,CO交⊙O于点D.若∠CAD=30°,则∠BOD=120°.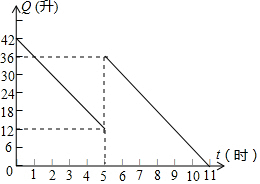 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.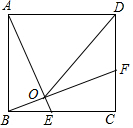 如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.
如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.