题目内容

15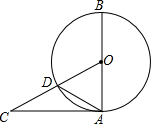．如图，AB是⊙O的直径，AC与⊙O相切，CO交⊙O于点D．若∠CAD=30°，则∠BOD=120°．

分析 根据切线的性质求出∠BAC=90°，求出∠OAD=60°，根据圆周角定理得出∠BOD=2∠BAD，代入求出即可．

解答 解：∵AC与⊙O相切，
∴∠BAC=90°，
∵∠CAD=30°，
∴∠OAD=60°，
∴∠BOD=2∠BAD=120°，
故答案为：120．

点评 本题考查了切线的性质和圆周角定理，能根据定理得出∠BAC=90°和∠BOD=2∠BAD是解此题的关键．

练习册系列答案
相关题目
5．如图，在直角坐标系中：
（1）写出△ABC各顶点的坐标；
（2）求△ABC的面积．
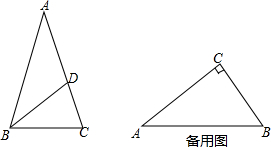6．我们知道，三角形的内心是三条角平分线的交点，过三角形内心的一条直线与两边相交，两交点之间的线段把这个三角形分成两个图形．若有一个图形与原三角形相似，则把这条线段叫做这个三角形的“內似线”．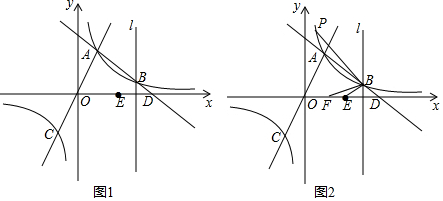
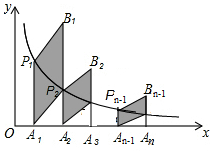（1）等边三角形“內似线”的条数为3；
（2）如图，△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求证：BD是△ABC的“內似线”；
（3）在Rt△ABC中，∠C=90°，AC=4，BC=3，E、F分别在边AC、BC上，且EF是△ABC的“內似线”，求EF的长．
3．在平面直角坐标系中，点P的坐标是（3，-2），则点P到x轴的距离为（　　）
A．2B．3C．-2D．-3
10．分解因式：9-b2=（3+b）（3-b）．
20．a、b是实数，点A（2，a）、B（3，b）在反比例函数y=-$\frac{2}{x}$的图象上，则（　　）
A．a＜b＜0B．b＜a＜0C．a＜0＜bD．b＜0＜a
7．如图1，一次函数y=-x+b与反比例函数y=$\frac{k}{x}$（k≠0）的图象交于点A（1，3），B（m，1），与x轴交于点D，直线OA与反比例函数y=$\frac{k}{x}$（k≠0）的图象的另一支交于点C，过点B作直线l垂直于x轴，点E是点D关于直线l的对称点．

（1）k=3；
（2）判断点B、E、C是否在同一条直线上，并说明理由；
（3）如图2，已知点F在x轴正半轴上，OF=$\frac{3}{2}$，点P是反比例函数y=$\frac{k}{x}$（k≠0）的图象位于第一象限部分上的点（点P在点A的上方），∠ABP=∠EBF，则点P的坐标为（$\frac{3}{2}$，$\frac{9}{2}$）．
14．我们知道：一个整数的个位数是偶数，则它一定能被2整除；一个整数的各位数字之和能被3整除，则它一定能被3整除．若一个整数既能被2整除又能被3整除，那么这个整数一定能被6整除．数字6象征顺利、吉祥，我们规定，能被6整除的四位正整数$\overline{abcd}$（千位数字为a，百位败字为b，十位数字为c，个位数字为d）是“吉样数”，请解答下面几个问题：
（1）已知$\overline{785x}$是“吉样数”，则x=4．
（2）若正整数$\overline{abcd}$是“吉样数”，试说明：d+4（a+b+c）能被2整除．
（3）小明完成第（2）问后认为：四位正整数$\overline{abcd}$是“吉样数”，邯么d+4（a+b+c）也是“吉祥数字”．你认为他说得对吗？请说明理由．
15．如图，分别过反比例函数y=$\frac{3}{x}$（x＞0）图象上的点P1（1，y1），P2（2，y2）…Pn（n，yn）作x轴的垂线，垂足分别为A1，A2，…An，连结A1P2，A2P3，…An-1Pn，再以A1P1，A1P2为一组邻边作平行四边形A1P1B1P2，以A2P2，A2P3为邻边作平行四边形A2P2B2P3，以此类推，则B1的纵坐标为$\frac{9}{2}$，Bn的纵坐标为$\frac{6n+3}{n（n+1）}$（用含n的代数式表示）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网