题目内容
9.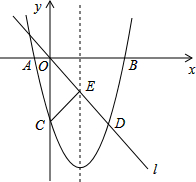 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线L经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线L经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).(1)求抛物线的函数表达式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE?若存在,请求出点F的坐标;若不存在,请说明理由.
分析 (1)把A、D坐标代入抛物线可求得抛物线的函数表达式,则抛物线的对称性可求得B点坐标,由D点坐标可求得直线OD的解析式,则可求得E点坐标;
(2)结合(1)可知OE=CE,由全等三角形的性质可知OF=CF,可知点F在线段OC的垂直平分线上,则可求得F点的纵坐标,代入抛物线解析式可求得F点的坐标.
解答 解:
(1)∵抛物线y=ax2+bx-8经过点A(-2,0),D(6,-8),
∴$\left\{{\begin{array}{l}{4a-2b-8=0\;\;\;\;}\\{36a+6b-8=-8}\end{array}}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-3}\end{array}\right.$,
∴抛物线的函数表达式为$y=\frac{1}{2}{x^2}-3x-8$;
∵$y=\frac{1}{2}{x^2}-3x-8=\frac{1}{2}{({x-3})^2}-\frac{25}{2}$,
∴抛物线的对称轴为直线x=3.
又抛物线与x轴交于A,B两点,点A的坐标为(-2,0).
∴点B的坐标为(8,0),
设直线L的函数表达式为y=kx.
∵点D(6,-8)在直线L上,
∴6k=-8,解得k=-$\frac{4}{3}$,
∴直线L的函数表达式为y=-$\frac{4}{3}$x,
∵点E为直线L和抛物线对称轴的交点,
∴点E的横坐标为3,纵坐标为-$\frac{4}{3}$×3=-4,
∴点E的坐标为(3,-4);
(2)抛物线上存在点F,使△FOE≌△FCE.
∵OE=CE=5,
∴FO=FC,
∴点F在OC的垂直平分线上,此时点F的纵坐标为-4,
∴$\frac{1}{2}$x2-3x-8=-4,解得x=3±$\sqrt{17}$,
∴点F的坐标为(3-$\sqrt{17}$,-4)或(3+$\sqrt{17}$,-4).
点评 本题为二次函数的综合应用,涉及待定系数法、二次函数的性质、全等三角形的性质、线段垂直平分线的判定等知识.在(1)中注意待定系数法的应用,在(2)中确定出点F在线段OC的垂直平分线上是解题的关键.本题考查知识点较多,难度适中.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| A. | 正数 | B. | 负数 | C. | 非负数 | D. | 无法确定 |
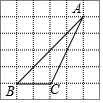 在正方形网格中,△ABC的位置如图所示,则tanB的值为( )
在正方形网格中,△ABC的位置如图所示,则tanB的值为( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
| A. | 8.50091×103 | B. | 8.50091×1011 | C. | 8.50091×105 | D. | 8.50091×1013 |
| A. | a2+4=(a+2)2 | B. | a2-2a+4=(a-2)2 | C. | x3-4x2=x2(x-4) | D. | 1-4x2=(1+4x)(1-4x) |
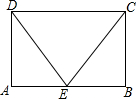 如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE.
如图,在矩形ABCD中,E分别是AB的一点,s△CDE=2SAEC,求证:△BEC≌△ADE.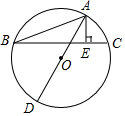 如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长.
如图,A,B,C为⊙O上的点,AD为⊙O的直径,AE⊥BC于E,AB=5,BE=$\sqrt{21}$,CE=$\sqrt{5}$,求AD的长. 如图,将?ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.
如图,将?ABCD的对角线BD向两个方向延长,分别至点E和点F,BE=DF.求证:四边形AECF是平行四边形.