题目内容
17.等腰三角形周长为20,一边长为4,则另两边长为8,8.分析 由于没有明确已知的边长是底还是腰,所以要分类讨论,最后要根据三角形三边关系定理来判断所求的解是否符号要求.
解答 解:当4为底时,腰长为:(20-4)÷2=8;8+4>8,能构成三角形;
∴另两边长为:8,8;
当4为腰时,底长为:20-4×2=12;4+4<12,不能构成三角形;
故答案为:8,8.
点评 本题考查了等腰三角形的性质和三角形的三边关系;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列各式有意义的条件下不一定成立的是( )
| A. | ${(\sqrt{a})^2}$=a | B. | $\sqrt{a^2}$=a | C. | $\root{3}{a^3}$=a | D. | $\root{3}{{-{a^3}}}$=-a |
9.用配方法解下列方程,其中应在左右两边同时加上4的是( )
| A. | x2-2x=5 | B. | x2-8x=4 | C. | x2-4x-3=0 | D. | x2+2x=5 |
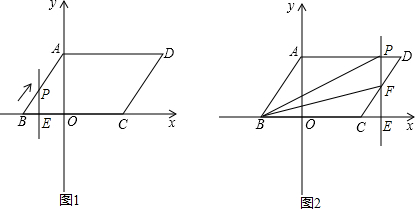
 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题: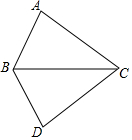 如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.
如图,∠ABC=∠DBC,请补充一个条件:AB=DB或∠A=∠D或∠ACB=∠DCB,使△ABC≌△DBC,并说明理由.