题目内容
16.(1)计算:$\sqrt{27}$+${(-\frac{1}{3})}^{-1}$+${(-\sqrt{2})}^{0}$-6sin60°(2)解不等式组$\left\{\begin{array}{l}{x-1>0}\\{3(x-1)<2x}\end{array}\right.$.
分析 (1)根据实数的混合运算顺序和法则计算即可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原式=3$\sqrt{3}$+(-3)+1-6×$\frac{\sqrt{3}}{2}$
=3$\sqrt{3}$-2-3$\sqrt{3}$
=-2;
(2)解不等式x-1>0,得:x>1,
解不等式3(x-1)<2x,得:x<3,
∴不等式组的解集为1<x<3.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
6.计算2-3的结果是( )
| A. | 1 | B. | 5 | C. | -5 | D. | -1 |
4.一个三角形的两边长分别为3和7,则第三边的长可能是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 11 |
8.对于抛物线y=ax2+4ax+m与x轴的交点为A(-1,0),B(x2,0),则下列说法:
①一元二次方程ax2+4ax+m=0的两根为x1=-1,x2=-3
②原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,则CD=4
③点E(1,y1),点F(-3,y2)在原抛物线上,则y2>y1
④抛物线y=ax2-4ax+m与原抛物线关于y轴对称.
其中正确的是( )
①一元二次方程ax2+4ax+m=0的两根为x1=-1,x2=-3
②原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,则CD=4
③点E(1,y1),点F(-3,y2)在原抛物线上,则y2>y1
④抛物线y=ax2-4ax+m与原抛物线关于y轴对称.
其中正确的是( )
| A. | ①②③④ | B. | ①②④ | C. | ①② | D. | ①②③ |
5.下列实数中最小的是( )
| A. | -4 | B. | -1 | C. | 0 | D. | $\sqrt{2}$ |
6.下列计算中正确的是( )
| A. | a3•a2=a6 | B. | 2a•a=2a2 | C. | (2a2)2=2a4 | D. | 6a8÷3a2=2a4 |
 如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标;
如图,已知直线l1:y=-2x+8与双曲线C:y=$\frac{6}{x}$(x>0),相交于点A和B(点A在点B的左上方),直线l2:y=kx(k>0)与直线l1相交于点C,于双曲线C相交于点D.(1)求点A、B的坐标; 如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.
如图,在平面直角坐标系中,已知点M(2,-3)、N(6,-3),连接MN,如果点P在直线y=-x+1上,且点P到直线MN的距离不小于1,那么称点P是线段MN的“疏远点”.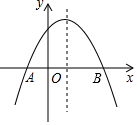 如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )
如图,抛物线y=ax2+bx+c,与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴交点在(0,2)、(0,3)之间(包含端点),有下列结论:①abc>0;②4ac-b2>0;③当x=3时,y=0;④3a+b>0;⑤-1≤a≤-$\frac{2}{3}$,;⑥$\frac{8}{3}$≤n≤4,其中正确的有( )