题目内容
10.某学校对学生进行体育测试,规定参加测试的每名学生从“1.立定跳远、2.1分钟跳绳3.掷实心球、4.50米跑”四个项目中随机抽取两项作为测试项目.(1)小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的概率是多少?
(2)据统计,初三一班共12名男生参加了“立定跳远”的测试,他们的成绩如下:
95 100 90 82 90 65 89 74 75 93 92 85
①这组数据的众数是90,中位数是89.5;
②若将不低于90分(含90分)的成绩评为优秀,请你估计初三年级选“立定跳远”的240名男生中成绩为优秀的学生约为多少人.
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的情况,再利用概率公式即可求得答案.
(2)①根据众数与中位数的定义求解即可求得答案;
②首先求得这12名男生中成绩为优秀的百分数,继而求得答案.
解答 解:(1)画树状图得: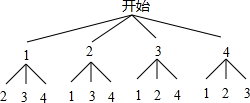
∵共有12种等可能的结果,小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的有2种情况,
∴小明同学恰好抽到“立定跳远”、“1分钟跳绳”两项的概率是:$\frac{2}{12}$=$\frac{1}{6}$;
(2)①这组数据的众数是90,中位数是$\frac{89+90}{2}$=89.5;
故答案为:90,89.5;
②∵这12名男生中,优秀的学生有6名,
∴初三年级选“立定跳远”的240名男生中成绩为优秀的学生约为:240×$\frac{6}{12}$=120(人).
点评 此题考查了列表法或树状图法求概率、用样本估计总体以及众数、中位数的定义.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
15. 如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )
如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )
 如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )
如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
20.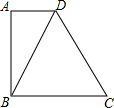 如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )
如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )
 如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )
如图所示,在四边形ABCD中,AB⊥BC,AB⊥AD,BD=BC,∠C=60°,如果△DBC的周长为m,则AD的长为( )| A. | $\frac{m}{3}$ | B. | $\frac{m}{6}$ | C. | $\frac{m}{8}$ | D. | $\frac{m}{12}$ |

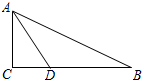 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于D.