题目内容
15. 如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )
如图,⊙O是△ABC的内切圆,切点分别是D、E、F.已知∠A=100°,∠C=40°,则∠DFE的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 根据三角形的内角和定理求得∠B=40°,再根据切线的性质以及四边形的内角和定理得出∠DOE=140°,再根据圆周角定理即可得出∠DFE=70°.
解答 解:∵∠A=100°,∠C=40°,
∴∠B=180°-∠A-∠C=40°,
∵⊙O是△ABC的内切圆,切点分别是D、E、F,
∴∠BDO=∠BEO=90°,
∴∠DOE=180°-∠B=140°,
∴∠DFE=$\frac{1}{2}$∠DOE=70°.
故选:D.
点评 本题考查了三角形的内切圆、切线的性质、圆周角定理、四边形内角和定理;熟练掌握切线的性质,求出∠DOE是解决问题的关键.

练习册系列答案
相关题目
3.当x=1时,代数式ax3+bx+5的值为-9,那么,当x=-1时,代数式ax3+bx+5的值为( )
| A. | 19 | B. | -9 | C. | 9 | D. | 1 |
20.下列事件中是必然事件的是( )
| A. | 平安夜下雪 | B. | 地球在自转的同时还不停的公转 | ||
| C. | 所有人15岁时身高必达到1.70米 | D. | 下雨时一定打雷 |
4.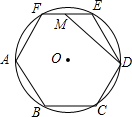 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
 如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为22cm.
如图,△ABC中,DE是AC的垂直平分线,AE=4cm,△ABD的周长为14cm,则△ABC的周长为22cm. 课堂上,左老师让同学们讨论一道题:如图,已知AB=AD,∠ABC=∠ADC.求证:BC=DC.
课堂上,左老师让同学们讨论一道题:如图,已知AB=AD,∠ABC=∠ADC.求证:BC=DC.