题目内容
1. 如图,两个正方形边长分别为a、b,如果a+b=18,ab=60,求图中阴影部分的面积.
如图,两个正方形边长分别为a、b,如果a+b=18,ab=60,求图中阴影部分的面积.
分析 由题意表示出AB,AD,CG、FG,进而表示出BG,阴影部分面积=正方形ABCD+正方形ECGF面积-三角形ABD面积-三角形FBG面积,求出即可.
解答 解:由题意得:AB=AD=a,CG=FG=b,BG=BC+CG=a+b,
∴S阴影=S正方形ABCD+S正方形ECGF-S直角△ABD-S直角△FBG
=AB•AD+CG•FG-$\frac{1}{2}$AB•AD-$\frac{1}{2}$BG•FG
=a2+b2-$\frac{1}{2}$a2-$\frac{1}{2}$(a+b)b
=$\frac{1}{2}$(a2+b2-ab)
=$\frac{1}{2}$[(a+b)2-3ab],
∵a+b=18,ab=60,
∴S阴影=$\frac{1}{2}$×(182-3×60)=72.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11. 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )| A. | 2.5 | B. | 2 | C. | 2.4 | D. | 3 |
9.下列实数中属于无理数的是( )
| A. | $\frac{23}{3}$ | B. | $\sqrt{1}$ | C. | 1.101001 | D. | -π |
6.三角形三边长分别为8,17,15,则最短边上的高为( )
| A. | 8 | B. | 15 | C. | 16 | D. | 17 |
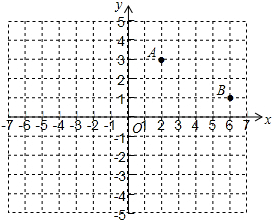 如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.
如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.