题目内容
20.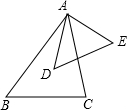 如图,若∠BAD=∠CAE,∠E=∠C,则△ABC∽△ADE.
如图,若∠BAD=∠CAE,∠E=∠C,则△ABC∽△ADE.
分析 利用“两角法”推知△ABC∽△ADE.
解答 解:如图,∵ ∠BAD=∠CAE,
∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
又∵∠E=∠C,
∴△ABC∽△ADE.
故答案是:△ABC;△ADE.
点评 本题考查了相似三角形的判定.(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
11. 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )| A. | 2.5 | B. | 2 | C. | 2.4 | D. | 3 |
5. 如图,已知∠ADB=∠CBD,下列所给条件不能证明△ABD≌△CDB的是( )
如图,已知∠ADB=∠CBD,下列所给条件不能证明△ABD≌△CDB的是( )
 如图,已知∠ADB=∠CBD,下列所给条件不能证明△ABD≌△CDB的是( )
如图,已知∠ADB=∠CBD,下列所给条件不能证明△ABD≌△CDB的是( )| A. | ∠A=∠C | B. | AD=BC | C. | ∠ABD=∠CDB | D. | AB=CD |
9.下列实数中属于无理数的是( )
| A. | $\frac{23}{3}$ | B. | $\sqrt{1}$ | C. | 1.101001 | D. | -π |
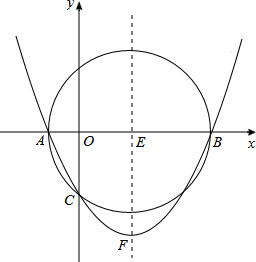 如图,已知以E(6,0)为圆心,以10为半径的⊙E与x轴交于A.B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F;
如图,已知以E(6,0)为圆心,以10为半径的⊙E与x轴交于A.B两点,与y轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F;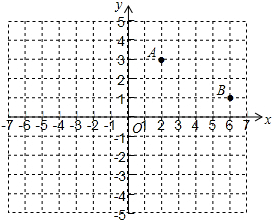 如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.
如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.