题目内容
3.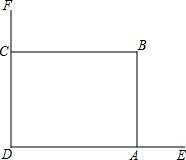 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).(1)如何才能围成矩形花园的面积为75m2?
(2)能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.
分析 (1)设BC=x米(0<x≤12),则AB=(20-x)米,利用矩形的面积公式列出方程并解答;
(2)解题思路同(1),列出方程,利用根的判别式的符号来判定方程的根的情况,即能否围成面积为101m2的矩形花园.
解答 解:(1)设BC=x米(0<x≤12),则AB=20-x米,
依题意得:x(20-x)=75,即x2-20x+75=0,
解得x1=5,x2=15(不合题意,舍去),
答:当BC=5米,AB=15米时,矩形的面积为75米2;
(2)不能围成面积为101m2的矩形花园,
因为:同(1)得,设BC=x米,得方程x(20-x)=101,即x2-20x+101=0△=b2-4ac=(-20)2-4×1×101=-4<0,
∴原方程无实根,
答:不能围成面积为101m2的矩形花园.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.注意x的取值范围.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
11. 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
 如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )
如图,在⊙O中,直径AB,弦CD,且AB⊥CD于点E,CD=4,OE=1.5,则⊙O的半径是( )| A. | 2.5 | B. | 2 | C. | 2.4 | D. | 3 |
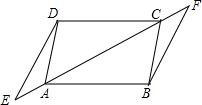 如图,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,试说明∠E=∠F.
如图,AD∥BC,AE=CF,AD=BC,E、F在直线AC上,试说明∠E=∠F.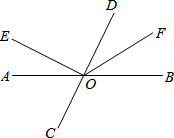 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.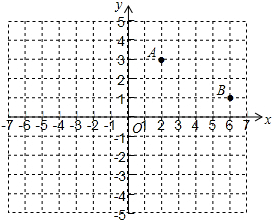 如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.
如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.