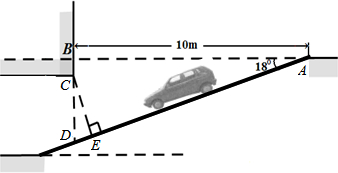
题目内容
问题:探索等腰三角形─腰上的高与底边所成的角与顶角的关系.
(1)为了解决这个问题,我们可从特殊情形入手,如图(1),△ABC中,AB=AC,∠A=40°,BD是AC边上的高,则∠DBC= °.如图(2),△ABC中,AB=AC,∠A=90°,BD是AC边上的高,则∠DBC= °.如图(3),△ABC中,AB=AC,∠A=120°,BD是AC边上的高,则∠DBC= °;
(2)猜想,∠A与∠DBC的关系是 ;
(3)对上述猜想,请你作出解释.

(1)为了解决这个问题,我们可从特殊情形入手,如图(1),△ABC中,AB=AC,∠A=40°,BD是AC边上的高,则∠DBC=
(2)猜想,∠A与∠DBC的关系是
(3)对上述猜想,请你作出解释.

考点:等腰三角形的性质
专题:探究型
分析:根据等腰三角形的性质和三角形内角和定理可求出等腰三角形的底角的度数,然后在一腰上的高与底边所构成的直角三角形中,可得出所求角的度数.
解答:解:(1)如图(1):△ABC中,AB=AC,BD是边AC上的高.
∵∠A=40°,且AB=AC,
∴∠ABC=∠C=(180°-40°)÷2=70°;
在Rt△BDC中,
∠BDC=90°,∠C=70°;
∴∠DBC=90°-70°=20°.
如图(2):△ABC中,AB=AC,BD是AC边上的高;
∵∠A=90°且AB=AC,
∴A点和D点重合;
在Rt△BDC中,∠BDC=90°;
∴∠DBC=90÷2=45°;
如图(3):△ABC中,AB=AC,BD是AC边上的高;
∵∠A=120°,且AB=AC,
∴∠ABC=∠C=(180°-120°)÷2=30°;
在Rt△BDC中,
∠BDC=90°,∠C=30°;
∴∠DBC=90°-30°=60°.
(2)根据以上的解答猜想;∠DBC=
∠A.
(3)在△ABC中,AB=AC,BD是边AC上的高,那
么∠ABC=∠ACB=(180°-∠A)÷2=90°-
∠A,
在Rt△BDC中,∠DBC=90°-(90°-
∠A)=
∠A.
∵∠A=40°,且AB=AC,
∴∠ABC=∠C=(180°-40°)÷2=70°;
在Rt△BDC中,
∠BDC=90°,∠C=70°;
∴∠DBC=90°-70°=20°.
如图(2):△ABC中,AB=AC,BD是AC边上的高;
∵∠A=90°且AB=AC,
∴A点和D点重合;
在Rt△BDC中,∠BDC=90°;
∴∠DBC=90÷2=45°;
如图(3):△ABC中,AB=AC,BD是AC边上的高;
∵∠A=120°,且AB=AC,
∴∠ABC=∠C=(180°-120°)÷2=30°;
在Rt△BDC中,
∠BDC=90°,∠C=30°;
∴∠DBC=90°-30°=60°.
(2)根据以上的解答猜想;∠DBC=
| 1 |
| 2 |
(3)在△ABC中,AB=AC,BD是边AC上的高,那
么∠ABC=∠ACB=(180°-∠A)÷2=90°-
| 1 |
| 2 |
在Rt△BDC中,∠DBC=90°-(90°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查等腰三角形的性质,及三角形内角和定理.求一个角的大小,常常通过三角形内角和来解决,注意应用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
已知m,n是方程x2-2
x+1=0的两根,则代数式
的值为( )
| 2 |
| m2+n2+3mn |
| A、3 | B、5 | C、9 | D、±3 |
 如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )
如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )A、(2,
| ||
| B、(4,2) | ||
C、(4,
| ||
D、(3,
|
 如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.
如图,已知抛物线y=-x2+2x+c经过点C(0,3),且与x轴交于A、B两点(点A在点B的左侧),线段BC与抛物线的对称轴相交于点P.M、N分别是线段OC和x轴上的动点,运动时保持∠MPN=90°不变.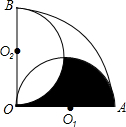 如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为
如图,扇形OAB的圆心角为90°、半径为2cm,半圆O1和半圆O2的直径分别为OA和OB,则图中阴影部分的面积为