题目内容
 如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )
如图,等边三角形OAB的边长为2,将它沿AB所在的直线对折,得到△O′AB,则点O的对应点O′的坐标是( )A、(2,
| ||
| B、(4,2) | ||
C、(4,
| ||
D、(3,
|
考点:翻折变换(折叠问题),坐标与图形性质,等边三角形的性质
专题:
分析:由折叠的性质和等边三角形的性质知OB=AO′,可先求出A点坐标,然后将A点坐标向右平移2个单位即可得到O′点的坐标.
解答: 解:过A作AD⊥x轴于D;
解:过A作AD⊥x轴于D;
在Rt△OAD中,OA=2,∠AOD=60°,则:
OD=1,AD=
;
∴A(1,
);
由折叠的性质和等边三角形的性质知:AO′=OB=2,
∴O′的坐标是(3,
).
故选:D.
 解:过A作AD⊥x轴于D;
解:过A作AD⊥x轴于D;在Rt△OAD中,OA=2,∠AOD=60°,则:
OD=1,AD=
| 3 |
∴A(1,
| 3 |
由折叠的性质和等边三角形的性质知:AO′=OB=2,
∴O′的坐标是(3,
| 3 |
故选:D.
点评:此题主要考查了等边三角形的性质、解直角三角形以及图象的翻折变换,能够根据折叠的性质得到AO′的长是解答此题的关键.

练习册系列答案
相关题目
 如图,该几何体的左视图是( )
如图,该几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
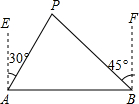 如图,城市A的正东方向100km处有一卫星城B,现计划在这两座城市间修筑一条城际快速通道(即线段AB),经测量,核能开发中心P在A城的北偏东30°和B城市的北偏西45°的方向上,已知核辐射区域是以P点为圆心50km为半径的圆形区域,请问这条快速通道会不会穿越核辐射区?请说明理由.
如图,城市A的正东方向100km处有一卫星城B,现计划在这两座城市间修筑一条城际快速通道(即线段AB),经测量,核能开发中心P在A城的北偏东30°和B城市的北偏西45°的方向上,已知核辐射区域是以P点为圆心50km为半径的圆形区域,请问这条快速通道会不会穿越核辐射区?请说明理由.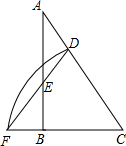 如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC=
如图,在Rt△ABC中,∠ABC=90°,以点C为圆心作弧,分别交AC、CB的延长线于点D、F,连结DF,交AB于点E,已知S△BEF=9,S△CDF=40,tan∠DFC=2,则BC= 如图,E是正方形ABCD中边CD上一点,且DE=
如图,E是正方形ABCD中边CD上一点,且DE=

 如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.
如图,某拦河坝横截面的原设计方案为梯形ABCD,其中AD∥BC,∠ABC=72°.为了提高拦河大坝的安全性,现将坝顶宽度水平缩短10m,坝底宽度水平增加4m,使∠EFC=45°.