题目内容

9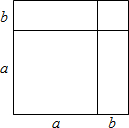．如图，大正方形的边长为a+b，用两种不同的方法计算这个大正方形的面积，可以推导出的公式是（　　）
A．（a+b）（a-b）=a2-b2B．（a+b）2=a2+2ab+b2C．（a-b）2=a2-2ab+b2D．（a+b）2-（a-b）2=4ab

分析 先根据大正方形的边长求出面积，再根据部分面积之和等于整体面积计算大正方形的面积，根据面积相等，列出等式，作出选择．

解答 解：∵大正方形的边长是a+b，
∴面积为：（a+b）2，
表示大正方形面积另一种方法：a2+ab+ab+b2=a2+2ab+b2
故选：B．

点评 本题是用数形结合的思想考查了证明完全平方公式，关键是准确的运用两种不同的方法表示出大正方形的面积，属于基础题．解答本题时，注意整体图形的面积等于各个部分的面积之和．

练习册系列答案
相关题目
19．如图，在△ABC中，AB=AC，∠A=40°，BD是∠ABC的平分线，求∠BDC的度数．
20．用代入法解三元一次方程组$\left\{\begin{array}{l}{2x+y+3z=13}\\{3x+2y-z=16}\\{x+3y-5z=10}\end{array}\right.$．
17．若等腰三角形的两边的长分别是5cm、7cm，则它的周长为17或19cm．
4．小明从家里骑自行车到学校，每小时骑15km，可早到10分钟，每小时骑12km就会迟到5分钟．问他家到学校的路程是多少km？设他家到学校的路程是xkm，则据题意列出的方程是A
A：$\frac{x}{15}+\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$  B：$\frac{x}{15}-\frac{10}{60}=\frac{x}{12}+\frac{5}{60}$  C：$\frac{x}{15}-\frac{10}{60}=\frac{x}{12}-\frac{5}{60}$   D$\frac{x}{15}+10=\frac{x}{12}-5$
导学探究
（1）路程，速度，时间的关系是路程=速度×时间
（2）规定的到校时间是$\frac{x}{15}$+$\frac{10}{60}$或$\frac{x}{12}$-$\frac{5}{60}$．
14．等腰三角形的周长为13cm，其中一边长为3cm，则该等腰三角形的底边为（　　）
A．7cmB．7cm或5cmC．5cmD．3cm
1．一列火车往返于芜湖、杭州两个城市，中途经过宣城、广德、长兴南和德清西4个站点（共6个站点），不同的车站往返需要不同的车票．
（1）共有多少种不同的车票？
（2）一列火车往返A、B两个城市，如果共有n（n≥3）个站点，则需要多少种不同的车票？
18．如图是一个正方形的展开图，每个面上都注明了字母，知道字母E的对面是D．
19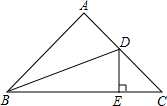．如图，在等腰Rt△ABC中，∠A=90°，AB=AC，BD平分∠ABC，交AC于点D，DE⊥BC，若BC=10cm，则△DEC的周长为（　　）
A．8cmB．10cmC．12cmD．14cm

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网