题目内容
4.已知:在正方形ABCD中,点P为对角线BD上一点,连接CP,作PE⊥PC交直线AB于E,作EQ⊥BD交直线BD于Q.(1)在图1中,当点P与对角线交点O重合时,易知点E,点Q都与点B重合,猜想CD与PQ的数量关系为CD=$\sqrt{2}$PQ;
(2)如图2,当P在线段DO上(不与D、O重合)移动时,(1)中的猜想还成立么,若成立,请证明;不成立请说明理由.
(3)当P在线段BO上(不与B、O重合)移动时,如图3,请你画出图形,(1)中的猜想还成立么,若成立,请直接写出结论;不成立请说明理由.

分析 (1)由正方形的性质得出AB=AD=BC=CD,OB=OC=OD,AC⊥BD,∠BDC=45°,得出△OBC是等腰直角三角形,证出CD=BC=$\sqrt{2}$OB=$\sqrt{2}$PQ;
(2)过点P作MN⊥AB于M,交CD于N,则MN=AD=CD=AB,△PDN是等腰直角三角形,∠MPE+MEP=90°,得出PN=DN,证出PM=CN,由角的互余关系证出∠MEP=∠NPC,由AAS证明△PEM≌△CPN,得出PE=CP,同理:△PEQ≌△CPO,由全等三角形的性质得出PQ=CO,即可得出CD=$\sqrt{2}$CO=$\sqrt{2}$PQ;
(3)同(2)得:△PEQ≌△CPO,得出PQ=CO,即可得出CD=$\sqrt{2}$CO=$\sqrt{2}$PQ
解答 解:(1)CD=$\sqrt{2}$PQ;理由如下:
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,OB=OC=OD,AC⊥BD,∠BDC=45°,
∴△OBC是等腰直角三角形,
∴CD=BC=$\sqrt{2}$OB=$\sqrt{2}$PQ;
故答案为:CD=$\sqrt{2}$PQ;
(2)成立;理由如下:
过点P作MN⊥AB于M,交CD于N,如图2所示:
则MN=AD=CD=AB,△PDN是等腰直角三角形,∠MPE+MEP=90°,
∴PN=DN,
∴PM=CN,
∵PE⊥PC,
∴∠MPE+∠NPC=90°,
∴∠MEP=∠NPC,
在△PEM和△CPN中,$\left\{\begin{array}{l}{∠EMP=∠PNC=90°}&{\;}\\{∠MEP=∠NPC}&{\;}\\{PM=CN}&{\;}\end{array}\right.$,
∴△PEM≌△CPN(AAS),
∴PE=CP,
同理:△PEQ≌△CPO,
∴PQ=CO,
∴CD=$\sqrt{2}$CO=$\sqrt{2}$PQ;
(3)成立;理由如下:如图3所示:
同(2)得:△PEQ≌△CPO,
∴PQ=CO,
∴CD=$\sqrt{2}$CO=$\sqrt{2}$PQ.
点评 本题是四边形综合题目,考查了正方形的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质等知识;本题综合性强,有一定难度,熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案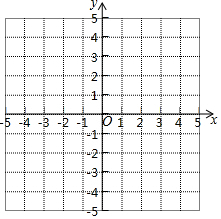 请按要求画出函数y=$\frac{1}{2}$x2的图象:
请按要求画出函数y=$\frac{1}{2}$x2的图象:(1)列表;
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | $\frac{9}{2}$ | 2 | $\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 2 | $\frac{9}{2}$ | … |
(3)连线;
(4)请你判断点(4,8)、(-$\frac{1}{2}$,-$\frac{1}{8}$)是否在函数图象上,答:点(4,8)在函数图象上,点(-$\frac{1}{2}$,-$\frac{1}{8}$)不在函数图象上.
| A. | 0 | B. | -1 | C. | 1 | D. | 2016 |
 如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.
如图,网格中每个小正方形的边长都为1,A、B、C都在格点上,试问△ABC是直角三角形吗?请说明理由.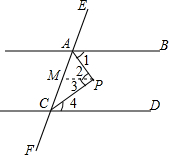 已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.
已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.