题目内容
17．
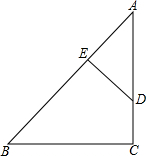如图，在Rt△ABC中，∠C=90°，DE⊥AB于E，$\frac{AD}{DC}$=$\frac{3}{2}$，AE•AB=15．则AC=5．
分析 首先判断△ABC∽△ADE，则可得AD：AB=AE：AC，由比例式得到AD•AC=AE•AB=15，由于$\frac{AD}{DC}$=$\frac{3}{2}$，设AD=3x，CD=2x，则AC=5x，于是得到3x•5x=15，即可得到结果．
解答 解：∵∠C=90°，DE⊥AB于E，
∴∠AED=∠ACB=90°，
∵∠A=∠A，
∴△ABC∽△ADE，
∴AD：AB=AE：AC，
∴AD•AC=AE•AB=15，
∵$\frac{AD}{DC}$=$\frac{3}{2}$，
设AD=3x，CD=2x，则AC=5x，
∴3x•5x=15，
∴x=1，
∴AC=5．
故答案为：5．
点评 本题考查了相似三角形的判定与性质，熟练掌握三角形相似的判定方法并把乘积式转化成比例式是解题的关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
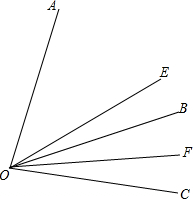已知：如图，OC是∠AOB外的一条射线，OE平分∠AOC，OF平分∠BOC．
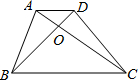如图所示，在梯形ABCD中，AD∥BC，AD=1，BC=3，△AOD，△AOB，△BOC的面积为S1，S2，S3，那么S1：S2：S3分别等于多少？